|
|
3. DEFINIZIONE
Sia
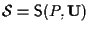 sottospazio affine di
sottospazio affine di
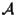 ,
spazio affine su ,
spazio affine su
 ; ricordiamo che assumiamo
; ricordiamo che assumiamo
 di dimensione finita per cui anche
di dimensione finita per cui anche
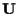 ha dimensione finita.
ha dimensione finita.
Definiamo la dimensione di 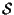 ponendo ponendo
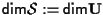 . .
Si noti che la definizione è ben posta grazie al risultato di esercizio 2.2
Se
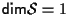
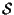 è detto "retta affine di
è detto "retta affine di
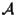 ". ".
Se
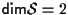
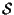 è detto "piano affine di
è detto "piano affine di
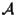 ". ".
Se
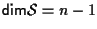
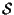 è detto "iperpiano affine di
è detto "iperpiano affine di
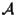 "
ove si è posto "
ove si è posto
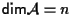 . .
Se
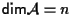 e
e
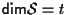 il numero naturale
il numero naturale 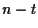 viene detto ''codimensione'' di
viene detto ''codimensione'' di
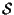 in
in
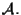
4. ESEMPI
4.1 Se consideriamo lo spazio affine 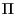 ,
il piano ordinario, abbiamo che punti, rette e ,
il piano ordinario, abbiamo che punti, rette e 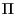 stesso sono i sottospazi affini di
stesso sono i sottospazi affini di 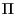 . .
Identicamente se consideriamo lo spazio affine 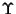 ,
lo spazio ordinario, abbiamo che punti, rette, piani e ,
lo spazio ordinario, abbiamo che punti, rette, piani e 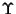 stesso sono i sottospazi affini di
stesso sono i sottospazi affini di 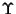 . .
4.2 Sia
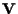 un
un
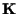 -spazio vettoriale; consideriamone la struttura affine (vedi esempio 5 della sezione "Spazi affini: definizione e proprietà"), cioè lo spazio affine -spazio vettoriale; consideriamone la struttura affine (vedi esempio 5 della sezione "Spazi affini: definizione e proprietà"), cioè lo spazio affine
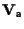 ;
siano ;
siano
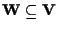 un sottospazio vettoriale e
un sottospazio vettoriale e
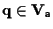 un punto.
un punto.
Consideriamo il sottospazio affine di
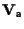 passante per
passante per
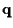 e con giacitura
e con giacitura
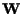 ; ;
per definizione si ha che
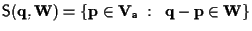 insieme che possiamo riscrivere come
insieme che possiamo riscrivere come
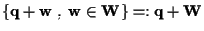 ,
infatti ,
infatti
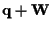 consiste proprio di tutti e soli i punti
consiste proprio di tutti e soli i punti
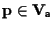 tali che
tali che
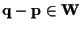 . .
 In particolare, se
In particolare, se
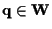 avremo che
avremo che
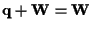 e dunque vediamo che i sottospazi vettoriali di
e dunque vediamo che i sottospazi vettoriali di
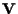 sono anche sottospazi affini di
sono anche sottospazi affini di
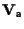 (e saranno tutti e soli i sottospazi passanti per il punto
(e saranno tutti e soli i sottospazi passanti per il punto
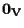 ). ).
Ricapitolando ogni sottospazio si può dunque sempre scrivere nella forma
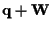 per un qualche punto
per un qualche punto
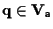 e
e
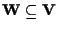 sottospazio vettoriale; esso è dunque il "traslato" di un sottospazio vettoriale.
sottospazio vettoriale; esso è dunque il "traslato" di un sottospazio vettoriale.
5. ESERCIZIO
Negli esercizi si determinano i sottospazi di dimensione minima e massima di uno spazio affine.

|
















 In particolare, se
In particolare, se


 _______________
_______________
 __
__
 _________________
_________________
