

 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

|

|
6. PROPOSIZIONE Sia
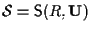 con
con
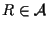 e
e
DIMOSTRAZIONE Sappiamo già che
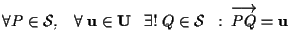 (ASS.1 in
(ASS.1 in
poiché in particolare
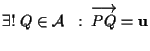 avendo usato ASS.1 in
avendo usato ASS.1 in
Infine dobbiamo dimostrare che
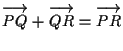 (uguaglianza fra vettori di
(uguaglianza fra vettori di
7. OSSERVAZIONE La dimensione di
8. OSSERVAZIONE
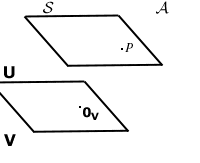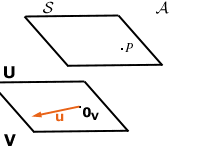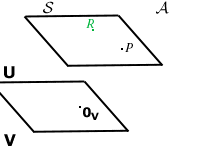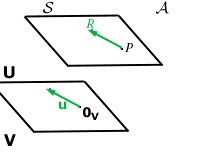
Fissando un punto in
![]() abbiamo una corrispondenza biunivoca tra i punti di
abbiamo una corrispondenza biunivoca tra i punti di
![]() e i vettori della sua giacitura e questo è un risultato generale per gli spazi affini (vedi punto 3 di proposizione 7 della sezione "Spazi affini: definizione e proprietà"); in particolare, poiché
e i vettori della sua giacitura e questo è un risultato generale per gli spazi affini (vedi punto 3 di proposizione 7 della sezione "Spazi affini: definizione e proprietà"); in particolare, poiché
![]() viene usualmente assegnato specificando anche un suo punto:
viene usualmente assegnato specificando anche un suo punto:
![]() ,
potremo dire che
,
potremo dire che
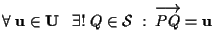
e viceversa
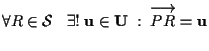 .
.
Questo fatto verrà usato ripetutamente in seguito.
9. ESERCIZIO
Nell'esercizio che segue si determina una condizione necessaria e sufficiente affinché un sottospazio sia contenuto in un altro sottospazio.


 _______________
_______________
 __
__
 ________________________
________________________