DEFINIZIONE DI APPLICAZIONE AFFINE

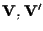
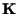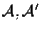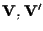1. DEFINIZIONE Siano $\mathbf{V},\mathbf{V}'$ $\mathbf{K}$ -spazi vettoriali e $\mathcal{A}, \mathcal{A}'$ spazi affini rispettivamente su $\mathbf{V},\mathbf{V}'$ .
Sia 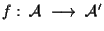$f:\; \mathcal{A} \;\longrightarrow \; \mathcal{A}'$ un'applicazione;

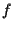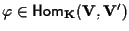è detta applicazione affine se esiste $\varphi \in \mathsf{Hom}_{\mathbf{K}}(\mathbf{V},\mathbf{V}')$ , detta parte lineare di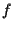

, tale che:

$\begin{displaymath}\overrightarrow{f(P)f(Q)}= \varphi (\overrightarrow{PQ})\;\;\;\;\forall\;P,Q\;\in \mathcal{A}\end{displaymath}$

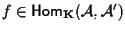Scriveremo $f \in \mathsf{Hom}_{\mathbf{K}}(\mathcal{A},\mathcal{A}')$ .

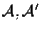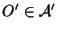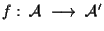Ad esempio: siano $\mathcal{A}, \mathcal{A}'$ spazi affini come al solito, $O' \in \mathcal{A}'$ ; definiamo $f:\; \mathcal{A} \;\longrightarrow \; \mathcal{A}'$ nel modo seguente: 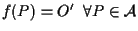$f(P)=O'\;\;\forall P \in \mathcal{A}$ , cioè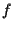

è costante. È banale dimostrare che

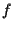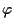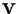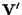è affine con parte lineare $\varphi$ l'applicazione "nulla" tra $\mathbf{V}$ e $\mathbf{V}'$ cioè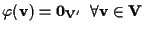

.

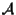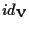2. ESERCIZI Negli esercizi si mostra che la parte lineare di un'applicazione affine è univocamente determinata e che le traslazioni di uno spazio affine $\mathcal{A}$ sono tutte e sole le applicazioni affini che hanno $id_{\mathbf{V}}$ come parte lineare.

______

_______________

________________________