|
|
Introduciamo ora in uno spazio affine astratto la nozione di parallelogramma, essa ci servirà nella dimostrazione del teorema di caratterizzazione geometrica dele affinità.
27. DEFINIZIONE
Sia
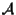 spazio affine,
spazio affine,
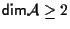 ; ;
siano
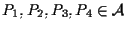 distinti e non collineari; poniamo
distinti e non collineari; poniamo
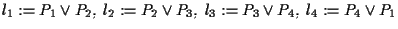 ;
se
accade che ;
se
accade che
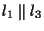 e
e
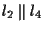 allora i punti
allora i punti
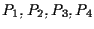 (in quest'ordine) sono detti vertici
(in quest'ordine) sono detti vertici
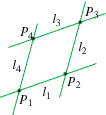 del parallelogramma di lati
del parallelogramma di lati
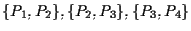 e
e
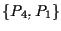 ;
indicheremo tale parallelogramma con il simbolo ;
indicheremo tale parallelogramma con il simbolo
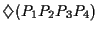 . .
I segmenti
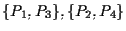 sono detti diagonali del parallelogramma .
sono detti diagonali del parallelogramma .
Si noti quindi che lati e diagonali sono segmenti non orientati, ma, riferendoci ad un parallelogramma, parliamo di una quaterna ordinata di punti.
28. PROPOSIZIONE
Sia
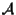 spazio affine,
spazio affine,
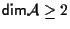 ; ;
consideriamo un parallelogramma
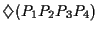 ,
allora ,
allora
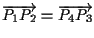 e
e
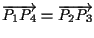 . .
DIMOSTRAZIONE
I vettori
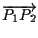 e
e
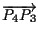 appartengono alla comune giacitura di
appartengono alla comune giacitura di 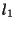 e
e 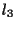 e dunque esiste
e dunque esiste
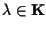 tale che
tale che
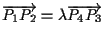 . .
Identicamente esiste
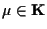 tale che
tale che
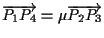 ,
dobbiamo quindi provare che ,
dobbiamo quindi provare che
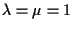 . .
A tal fine si osservi che
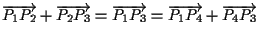 da cui
da cui
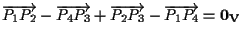 uguaglianza che possiamo
riscrivere come:
uguaglianza che possiamo
riscrivere come:
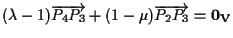 .
Ma .
Ma
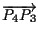 e
e
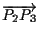 sono vettori linearmente indipendenti (e di qui
sono vettori linearmente indipendenti (e di qui
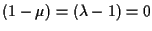 ),
infatti sono non
nulli e stanno su 2 rette vettoriali ),
infatti sono non
nulli e stanno su 2 rette vettoriali
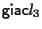 , ,
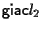 che sono distinte (se cosí non fosse allora
che sono distinte (se cosí non fosse allora 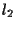 e
e 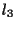 sarebbero parallele,
ma esse si intersecano in
sarebbero parallele,
ma esse si intersecano in 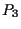 e quindi sarebbero coincidenti contro l'ipotesi di non collinearità dei 4 punti
e quindi sarebbero coincidenti contro l'ipotesi di non collinearità dei 4 punti
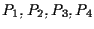 ). ).
29. ESERCIZI
L'esercizio proposto ci servirà come lemma nella dimostrazione del teorema di caratterizzazione geometrica delle affinità.

|



















 del parallelogramma di lati
del parallelogramma di lati


 _______________
_______________
 __
__
 ________________________
________________________