IMMAGINE E CONTROIMMAGINE DI UN SOTTOSPAZIO TRAMITE UN'APPLICAZIONE AFFINE

9. PROPOSIZIONE Siano $\mathbf{V},\mathbf{V}'$ $\mathbf{K}$ -spazi vettoriali e $\mathcal{A}, \mathcal{A}'$ spazi affini rispettivamente su $\mathbf{V},\mathbf{V}'$ e sia $f:\;\mathcal{A}\longrightarrow\mathcal{A}'$ applicazione affine e sia $\Phi(f)=:\varphi$ la sua parte lineare.

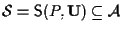Sia $\mathcal{S}=\mathsf{S}(P,\mathbf{U})\subseteq\mathcal{A}$ sottospazio affine, allora 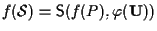$f(\mathcal{S})=\mathsf{S}(f(P),\varphi(\mathbf{U}))$ , in particolare l'immagine di un sottospazio affine tramite un'applicazione affine è ancora un sottospazio affine.
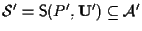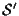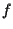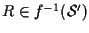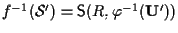Sia $\mathcal{S}'=\mathsf{S}(P',\mathbf{U}')\subseteq\mathcal{A}'$ sottospazio affine; supponiamo che la controimmagine di $\mathcal{S}'$ tramite sia non vuota e sia $R\in f^{-1}(\mathcal{S}')$ ; allora vale: $f^{-1}(\mathcal{S}')=\mathsf{S}(R,\varphi^{-1}(\mathbf{U}'))$ , in particolare la controimmagine di un sottospazio affine tramite un'applicazione affine, se non vuota, è ancora un sottospazio affine.

DIMOSTRAZIONE

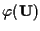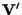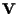Innanzitutto giustifichiamo l'ultima affermazione ricordando che $\varphi(\mathbf{U})$ è sottospazio vettoriale di $\mathbf{V}'$ in quanto immagine tramite un'applicazione lineare di un sottospazio vettoriale di $\mathbf{V}$ .
Procediamo alla dimostrazione della "doppia inclusione":
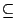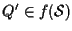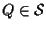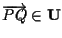$\subseteq$ ) Sia $Q' \in f(\mathcal{S})$ , esiste cioè $Q \in \mathcal{S}$ -ossia $\overrightarrow{PQ}\in \mathbf{U}$ - tale che .
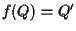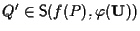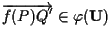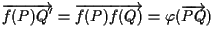Vorremmo $Q' \in \mathsf{S}(f(P),\varphi(\mathbf{U}))$ , cioè $\overrightarrow{f(P)Q'}\in \varphi(\mathbf{U})$ , e questo segue dall'uguaglianza $\overrightarrow{f(P)Q'}=\overrightarrow{f(P)f(Q)}=\varphi(\overrightarrow{PQ})$ per definizione di applicazione affine.

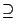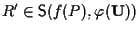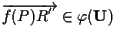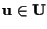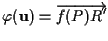$\supseteq$ ) Sia $R' \in \mathsf{S}(f(P),\varphi(\mathbf{U}))$ cioè $\overrightarrow{f(P)R'\;}\in \varphi(\mathbf{U})$ , esiste dunque $\mathbf{u}\in\mathbf{U}$ tale che $\varphi(\mathbf{u})=\overrightarrow{f(P)R'}$ .
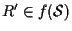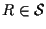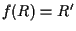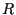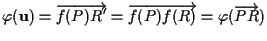Vorremmo che $R' \in f(\mathcal{S})$ , vorremmo cioè trovare $R \in \mathcal{S}$ tale che . Se un siffatto esiste allora vale $\varphi(\mathbf{u})=\overrightarrow{f(P)R'}=\overrightarrow{f(P)f(R)}=\varphi(\overrightarrow{PR})$ .
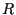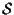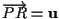Prendiamo spunto da questo fatto per definire come quel punto di $\mathcal{S}$ tale che $\overrightarrow{PR}=\mathbf{u}$ . Verifichiamo che effettivamente :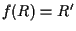
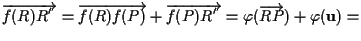
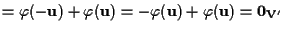. E ciò conclude la dimostrazione.
L'ultima affermazione è giustificata dal fatto che la controimmaggine di un sottospazio vettoriale tramite un'applicazione lineare è sempre un sottospazio vettoriale (perché non è mai vuoto?). A questo punto procediamo alla dimostrazione della doppia inclusione:

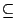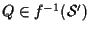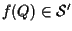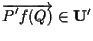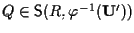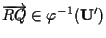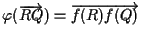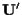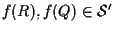$\subseteq$ ) Sia $Q \in f^{-1}(\mathcal{S}')$ , cioè $f(Q)\in\mathcal{S}'$ , ossia $\overrightarrow{P'f(Q)}\in\mathbf{U}'$ ; vorremmo $Q \in \mathsf{S}(R,\varphi^{-1}(\mathbf{U}'))$ , cioè , cioè ; d'altra parte , vettore che sta effettivamente in dato che $f(R),f(Q)\in \mathcal{S}'$ .
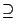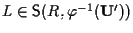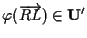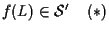$\supseteq$ ) Viceversa, se $L \in \mathsf{S}(R,\varphi^{-1}(\mathbf{U}'))$ , cioè $\varphi(\overrightarrow{RL})\in\mathbf{U}'$ , dobbiamo dimostrare che $f(L)\in\mathcal{S}'\;\;\;\;(\ast)$ .
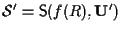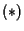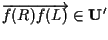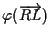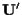Ricordando esercizio 2.4 della sezione "Sottospazi affini", potremo certamente scrivere $\mathcal{S}'=\mathsf{S}(f(R),\mathbf{U}')$ per cui la condizione $(\ast)$ si potrà esprimere dicendo: $\overrightarrow{f(R)f(L)}\in\mathbf{U}'$ e ciò è vero in quanto dalla definizione di applicazione affine tale vettore è $\varphi(\overrightarrow{RL})$ che sappiamo stare in $\mathbf{U}'$ .

10. ESERCIZI Negli esercizi si vede com'è fatta l'immagine di sottospazi generati da punti.

______

_______________

________________________