UN'APPLICAZIONE AFFINE È UNIVOCAMENTE DETERMINATA SE DATO IL VALORE SU n+1 PUNTI INDIPENDENTI

In definitiva abbiamo ottenuto dal teorema precedente che la condizione "essere applicazione affine" è molto rigida ricordando quanto lo era la condizione "essere applicazione lineare"; queste ultime, ricordiamolo, sono univocamente determinate se assegnate sui vettori di una base e quindi ora un'applicazione affine sarà univocamente determinata se è assegnato il suo valore su un punto e della sua parte lineare sono assegnati i valori su una base dello spazio vettoriale soggiacente.
È però piú elegante operare direttamente sui punti dello spazio affine come chiarito dalla seguente proposizione:

8. PROPOSIZIONE Siano

$\mathbf{K}$ -spazi vettoriali e $\mathcal{A}, \mathcal{A}'$ spazi affini rispettivamente su $\mathbf{V},\mathbf{V}'$ e sia $\mathsf{dim}\mathcal{A}=n$ .
Siano $P_0,P_1,\ldots, P_n\in\mathcal{A}$ punti indipendenti
(vedi definizione 19 della sezione "Sottospazi affini") e
siano 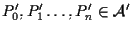$P'_0,P'_1,\ldots, P'_n\in\mathcal{A}$ punti arbitrari.
Allora esiste un'unica $f:\; \mathcal{A} \longrightarrow \mathcal{A}'$ applicazione affine tale che $f(P_i)=P'_i\;\;,\;\;i=0,1,\ldots,n$ .

DIMOSTRAZIONE Noi sappiamo che gli

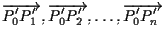vettori $\overrightarrow{P_0 P_1},\overrightarrow{P_0 P_2},\dots,\overrightarrow{P_0 P_n}$ formano una base di $\mathbf{V}$ (vedi osservazione 20 della sezione "Sottospazi affini") e consideriamo anche gli

vettori di $\mathbf{V}'$ $\overrightarrow{P'_0 P'_1},\overrightarrow{P'_0 P'_2},\dots,\overrightarrow{P'_0 P'_n\;}$ .
Dall'algebra lineare sappiamo che esiste un'unica applicazione lineare $\varphi:\;\mathbf{V}\longrightarrow\mathbf{V}'$ tale che $\varphi(\overrightarrow{P_0 P_i})=\overrightarrow{P'_0 P'_i}\;\;,\;\;i=1,\ldots,n$ ; $\varphi$ sarà la parte lineare di

.
Determiniamo

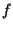come nel teorema precedente, cioè come quell'applicazione affine che ha $\varphi$ come parte lineare e che porta ad esempio

; poiché

è applicazione affine si ha che $\overrightarrow{P'_0 f(P)}=\varphi(\overrightarrow{P_0 P})$ per ogni punto

.
Resta da dimostrare che $f(P_i)=P'_i\;\;,\;\;i=1,\ldots,n$ : $\overrightarrow{P'_i f(P_i)}=\overrightarrow{P'_i P'_0\;}+\overrightarrow{P'_0... ...ightarrow{P'_i P'_0\;}+\overrightarrow{P'_0 P'_i\;\;}=\mathbf{0}_{\mathbf{V}'}$ e ciò conclude la dimostrazione.

______

_______________

________________________