|
|
Segue dalla definizione che un'applicazione affine 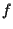 tra
tra
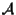 e
e
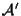 determina un'applicazione lineare
determina un'applicazione lineare
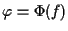 tra
tra
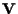 e
e
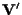 ;
d'altra parte sappiamo che possono esistere diverse applicazioni affini aventi la stessa parte lineare (ad esempio le traslazioni) e quindi la conoscenza della parte lineare non determina l'applicazione affine stessa; effettivamente non serve molto di piú: basta anche conoscere come l'applicazione affine agisce su un punto, come chiarito dalla proposizione seguente: ;
d'altra parte sappiamo che possono esistere diverse applicazioni affini aventi la stessa parte lineare (ad esempio le traslazioni) e quindi la conoscenza della parte lineare non determina l'applicazione affine stessa; effettivamente non serve molto di piú: basta anche conoscere come l'applicazione affine agisce su un punto, come chiarito dalla proposizione seguente:
7. TEOREMA
Siano
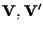
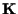 -spazi vettoriali e -spazi vettoriali e
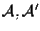 spazi affini rispettivamente su
spazi affini rispettivamente su
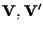 . .
Siano inoltre
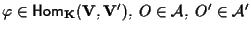 ; ;
allora esiste un'unica applicazione affine
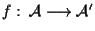 tale che
tale che 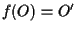 e
e
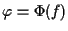 . .
DIMOSTRAZIONE
Supponiamo che 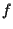 esista: allora
esista: allora
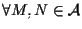 deve valere
deve valere
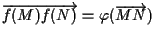 ,
in particolare scegliendo ,
in particolare scegliendo 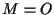 otterremo
otterremo
Dati
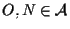 e quindi un vettore
e quindi un vettore
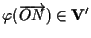 e un punto
e un punto
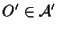 ,
esiste un unico punto ,
esiste un unico punto 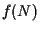 in
in
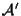 che soddisfa l'identità
che soddisfa l'identità 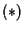 -è il contenuto di ASS.1 di spazio affine-
(punto che dipende da -è il contenuto di ASS.1 di spazio affine-
(punto che dipende da
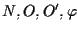 ,
ma ,
ma
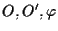 sono fissati per cui potremo indicare solo la dipendenza da
sono fissati per cui potremo indicare solo la dipendenza da 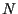 ,
venendosi cosí effettivamente a definire una funzione ,
venendosi cosí effettivamente a definire una funzione
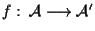 ). ).
In virtú di ciò possiamo dire che se 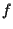 esiste allora è unica.
esiste allora è unica.
Proviamo a definire 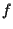 proprio in questa maniera e verifichiamo le richieste:
proprio in questa maniera e verifichiamo le richieste:
Si osservi che in particolare otteniamo che l'applicazione
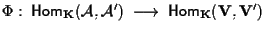 è sempre suriettiva e in generale non iniettiva (perché in generale? in quale caso è anche iniettiva?)
è sempre suriettiva e in generale non iniettiva (perché in generale? in quale caso è anche iniettiva?)
|













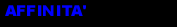


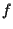 applicazione affine,
applicazione affine,
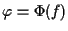 :
:
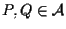 ,
abbiamo che
,
abbiamo che
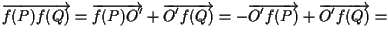
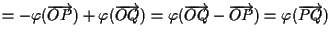
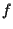 porta
porta 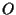 in
in 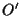 :
:
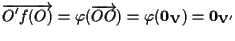 e questo implica
e questo implica 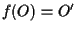 .
.

 _______________
_______________
 __
__
 ________________________
________________________