|
|

|

|
Come nel caso delle applicazioni lineari è naturale considerare quelle applicazioni affini che sono biunivoche:
3. DEFINIZIONE
Siano 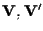
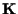 -spazi vettoriali e -spazi vettoriali e
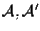 spazi affini rispettivamente su
spazi affini rispettivamente su
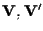 . .
Un'applicazione affine
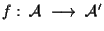 è detta isomorfismo affine se biunivoca.
è detta isomorfismo affine se biunivoca.
Scriveremo
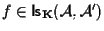 . .
Se
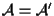
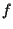 è detta affinità e scriveremo
è detta affinità e scriveremo
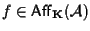 . .
4. PROPOSIZIONE
Un'applicazione affine è un isomorfismo affine se e solo se la sua parte lineare è un isomorfismo di
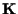 -spazi vettoriali. -spazi vettoriali.
DIMOSTRAZIONE
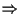 )
Sia )
Sia
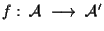 applicazione affine biunivoca; dobbiamo dimostrare che
applicazione affine biunivoca; dobbiamo dimostrare che
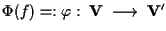 è isomorfismo di
è isomorfismo di
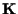 -spazi vettoriali; per definizione -spazi vettoriali; per definizione 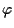 è lineare allora basterà dimostrare che è biunivoca.
è lineare allora basterà dimostrare che è biunivoca.
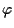 iniettiva: sia
iniettiva: sia
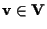 tale che
tale che
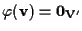 ;
vogliamo dimostrare che ;
vogliamo dimostrare che
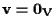 ;
sicuramente possiamo trovare ;
sicuramente possiamo trovare
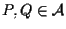 tali che
tali che
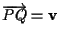 ;
ora si ha ;
ora si ha
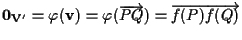 per definizione di applicazione affine; allora
per definizione di applicazione affine; allora 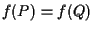 ,
ma ,
ma 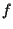 è iniettiva e dunque
è iniettiva e dunque 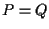 da cui
da cui
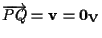 . .
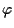 suriettiva: sia
suriettiva: sia
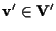 ;
vorremmo trovare ;
vorremmo trovare
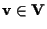 tale che
tale che
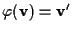 ;
ora siano ;
ora siano
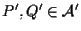 tali che
tali che
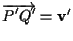 ; ;
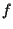 è suriettiva allora esistono
è suriettiva allora esistono
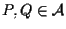 tali che
tali che 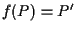 e
e 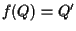 .
Ora si ha .
Ora si ha
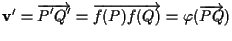 per cui ponendo
per cui ponendo
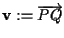 siamo a posto.
siamo a posto.
 )
Sia )
Sia
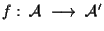 applicazione affine e sia
applicazione affine e sia
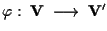 , la sua parte lineare, isomorfismo di , la sua parte lineare, isomorfismo di
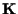 -spazi vettoriali; dobbiamo dimostrare che -spazi vettoriali; dobbiamo dimostrare che 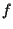 è biunivoca.
è biunivoca.
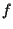 iniettiva: siano
iniettiva: siano
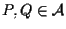 tali che
tali che 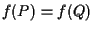 ;
vorremmo ;
vorremmo 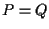 ;
ora si ha ;
ora si ha
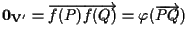 e siccome
e siccome 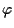 è lineare e iniettiva abbiamo che
è lineare e iniettiva abbiamo che
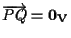 cioè proprio
cioè proprio 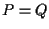 . .
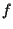 suriettiva: sia
suriettiva: sia
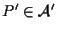 ,
vorremmo trovare ,
vorremmo trovare
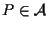 tale che
tale che 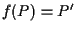 ;
sia ;
sia
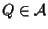 arbitrario, poniamo
arbitrario, poniamo 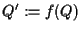 e consideriamo il vettore
e consideriamo il vettore
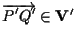 ;
siccome ;
siccome 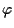 è suriettiva possiamo trovare
è suriettiva possiamo trovare
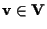 tale che
tale che
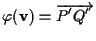 ;
per ASS.1 di spazio affine ;
per ASS.1 di spazio affine
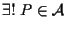 tale che
tale che
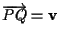 ;
affermiamo che ;
affermiamo che 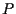 fa al caso nostro:
fa al caso nostro:
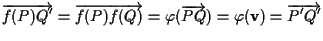 e questo implica (vedi esercizio 8.3 della sezione "Spazi affini: definizione e proprietà")
e questo implica (vedi esercizio 8.3 della sezione "Spazi affini: definizione e proprietà") 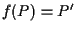 . .
5. COROLLARIO
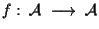 è affinità se e solo se la sua parte lineare è un automorfismo di
è affinità se e solo se la sua parte lineare è un automorfismo di
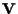 . .
6. ESERCIZI
L'esercizio proposto tratta alcune proprietà della relazione "essere isomorfo" .

|















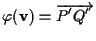 ;
per ASS.1 di spazio affine
;
per ASS.1 di spazio affine
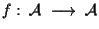 è affinità se e solo se la sua parte lineare è un automorfismo di
è affinità se e solo se la sua parte lineare è un automorfismo di


 _______________
_______________
 __
__
 ________________________
________________________