DECOMPOSIZIONE DI UN'AFFINITÀ:

26. TEOREMA Sia $\mathcal{A}$ spazio affine su $\mathbf{V}$ , $O\in\mathcal{A}$ e $f\in \mathsf{Aff}_{\mathbf{K}}(\mathcal{A})$ .
Esistono unici $\mathbf{v} \in \mathbf{V}$ e $g\in\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})_{O}$ tali che $f= \mathsf{T}_{\mathbf{v}}\circ g$ .

DIMOSTRAZIONE Come sempre supponiamo che $\mathbf{v}$ e

esistano e vediamo come devono essere fatti:
sia $P\in\mathcal{A}$ , posto $f(P)=\mathsf{T}_{\mathbf{v}}(g(P))=:Q$ abbiamo per definizione di traslazione che $\overrightarrow{g(P)Q}=\mathbf{v}$ , per cui se esiste $\mathbf{v}$ è univocamente determinato:
infatti anche

(cioè

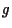) è univocamente determinato dalla condizione 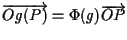$\overrightarrow{Og(Q)}=\Phi(g)(\overrightarrow{OP})$ cioè essere un'applicazione affine e fissare il punto

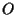perché $\Phi(g)$ non è arbitrario: $\varphi:=\Phi(f)=\Phi(\mathsf{T}_{\mathbf{v}}\circ g)=\Phi(\mathsf{T}_{\mathbf{v}})\circ\Phi( g)=id_{\mathbf{V}}\circ \Phi(g)=\Phi( g)$ .

A questo punto ci si può immaginare come definire $\mathsf{T}_{\mathbf{v}}$ e

: definiamo

in modo tale che $\overrightarrow{Og(P)}=\varphi(\overrightarrow{OP})$ e sappiamo già che $g\in\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})_{O}$ (si confronti con la dimostrazione di teorema 7) e definiamo $\mathbf{v}:=\overrightarrow{g(O)f(O)}=\overrightarrow{Of(O)}$ .

A questo punto non resta che verificare che tali scelte sono effettivamente "azzeccate": poiché

e $\mathsf{T}_{\mathbf{v}}\circ g$ hanno la stessa parte lineare basterà verificare che coincidono su un punto; scegliamo

: $\mathsf{T}_{\mathbf{v}}(g(O))=\mathsf{T}_{\mathbf{v}}(O)$ e $\mathsf{T}_{\mathbf{v}}(O)=f(O)\;\Leftrightarrow\; \overrightarrow{Of(O)}=\mathbf{v}$ e ciò è esattamente quanto accade.

______

_______________

________________________