GRUPPO DELLE AFFINITÀ E SUOI SOTTOGRUPPI

22. ESERCIZI In questo paragrafo andrebbe innanzitutto risolto l'esercizio proposto

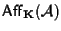in cui si afferma che $\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})$ è gruppo rispetto alla composizione; nel seguito si esaminano alcuni suoi importanti sottogruppi.

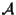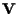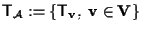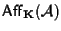23. PROPOSIZIONE Sia $\mathcal{A}$ spazio affine su $\mathbf{V}$ ; l'insieme delle traslazioni $\mathsf{T}_{\mathcal{A}}:=\{\mathsf{T}_{\mathbf{v}},\;\mathbf{v}\in\mathbf{V}\}$ è sottogruppo commutativo di $\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})$ ;
inoltre l'applicazione

$\begin{displaymath}\begin{array}{ccc} \mathbf{V} & \longrightarrow & \mathsf{T}_... ... \\ \mathbf{v} & \mapsto & \mathsf{T}_{\mathbf{v}} \end{array}\end{displaymath}$

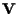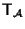dà un isomorfismo tra il gruppo additivo di $\mathbf{V}$ e $\mathsf{T}_{\mathcal{A}}$ .

DIMOSTRAZIONE Dimostriamo che 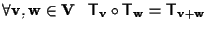$\forall \mathbf{v}, \mathbf{w} \in \mathbf{V}\;\;\;\mathsf{T}_{\mathbf{v}}\circ\mathsf{T}_{\mathbf{w}}=\mathsf{T}_{\mathbf{v}+\mathbf{w}}$ ; da ciò conseguirà che la composizione di traslazioni è traslazione e che si tratta di un' operazione interna commutativa.
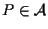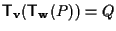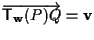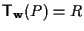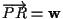Se $P \in \mathcal{A}$ , dire che $\mathsf{T}_{\mathbf{v}}(\mathsf{T}_{\mathbf{w}}(P))=Q$ significa che $\overrightarrow{\mathsf{T}_{\mathbf{w}}(P)Q}=\mathbf{v}$ (ed ancora $\mathsf{T}_{\mathbf{w}}(P)=R$ significa che $\overrightarrow{PR}=\mathbf{w}$ per definizione di traslazione).
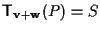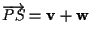Poniamo $\mathsf{T}_{\mathbf{v}+\mathbf{w}}(P)=S$ ossia $\overrightarrow{PS}=\mathbf{v}+\mathbf{w}$ , dobbiamo dimostrare quindi che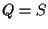

; e infatti si ha:
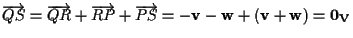$\overrightarrow{QS}=\overrightarrow{QR}+\overrightarrow{RP}+\overrightarrow{PS}=-\mathbf{v}-\mathbf{w}+(\mathbf{v}+\mathbf{w})=\mathbf{0}_{\mathbf{V}}$ .
A questo punto dobbiamo dimostrare che 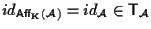$id_{\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})}=id_{\mathcal{A}}\in \mathsf{T}_{\mathcal{A}}$ e che l'inverso di ogni traslazione è ancora una traslazione.
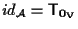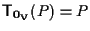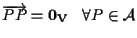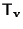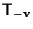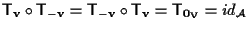Affermiamo che vale $id_{\mathcal{A}}=\mathsf{T}_{\mathbf{0}_{\mathbf{V}}}$ infatti $\mathsf{T}_{\mathbf{0}_{\mathbf{V}}}(P)=P$ poiché $\overrightarrow{PP}=\mathbf{0}_{\mathbf{V}}\;\;\;\forall P \in \mathcal{A}$ e inoltre che l'inverso di $\mathsf{T}_{\mathbf{v}}$ è $\mathsf{T}_{-\mathbf{v}}$ infatti $\mathsf{T}_{\mathbf{v}}\circ\mathsf{T}_{-\mathbf{v}}=\mathsf{T}_{-\mathbf{v}}\circ\mathsf{T}_{\mathbf{v}}=\mathsf{T}_{\mathbf{0}_{\mathbf{V}}}=id_{\mathcal{A}}$ .
A questo punto l'applicazione 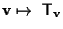$\mathbf{v}\mapsto\ \mathsf{T}_{\mathbf{v}}$ diviene banalmente un isomorfismo di gruppi.

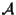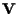Sia $\mathcal{A}$ spazio affine su $\mathbf{V}$ ; abbiamo visto che l'applicazione

$\begin{displaymath}\begin{array}{lccc} \Phi:& \mathsf{Aff}_{\mathbf{K}}(\mathcal... ...thsf{GL}(\mathbf{V}) \\ \;& f & \mapsto & \Phi(f) \end{array}\end{displaymath}$

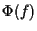ove $\Phi(f)$ è la parte lineare di

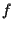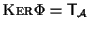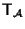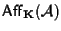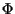, è un epimorfismo di gruppi (vedi commento in esercizio 22); in questi termini il risultato dell'esercizio 2.2 ci dice che $\mbox{\textsc{Ker}}\Phi=\mathsf{T}_{\mathcal{A}}$ per cui $\mathsf{T}_{\mathcal{A}}$ è un sottogruppo normale di $\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})$ ; inoltre, poiché $\Phi$ è suriettivo, potremo scrivere

$\begin{displaymath}\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})/\mathsf{T}_{\mathcal{A}} \cong \mathsf{GL}(\mathbf{V})\end{displaymath}$

.

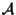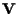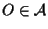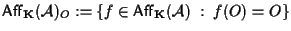24. DEFINIZIONE-PROPOSIZIONE $\mathcal{A}$ spazio affine su $\mathbf{V}$ e sia $O \in \mathcal{A}$ ; definiamo $\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})_{O}:=\{f\in\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})\;:\;f(O)=O\}$ ; si tratta cioè dell'insieme delle affinità che lasciano fisso il punto O.
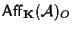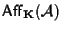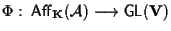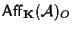Affermiamo che $\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})_{O}$ è un sottogruppo di $\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})$ e che l'epimorfismo di gruppi $\Phi:\;\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})\longrightarrow\mathsf{GL}(\mathbf{V})$ induce in isomorfismo se ristretto ad $\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})_{O}$ .

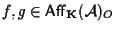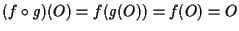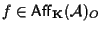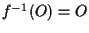DIMOSTRAZIONE Siano $f,g\in\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})_{O}$ , allora $(f\circ g)(O)=f(g(O))=f(O)=O$ ; se $f\in\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})_{O}$ allora $f^{-1}(O)=O$ perché

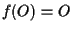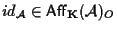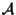; infine $id_{\mathcal{A}}\in\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})_{O}$ infatti fissa ogni punto di $\mathcal{A}$ .

Considerata 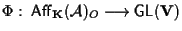$\Phi:\;\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})_{O}\longrightarrow\mathsf{GL}(\mathbf{V})$ basta dimostrare che 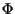$\Phi$ è biunivoca cioè che 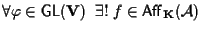$\forall \varphi\in\mathsf{GL}(\mathbf{V})\;\;\exists !\;f\in\mathsf{Aff}_{\mathbf{K}}(\mathcal{A})$ tale che 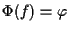$\Phi(f)=\varphi$ e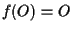

e questo segue da teorema 7.

______

_______________

________________________