

 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

|

|
25. DEFINIZIONE-PROPOSIZIONE Sia
Consideriamo l'isomorfismo
Essa è detta omotetia di centro
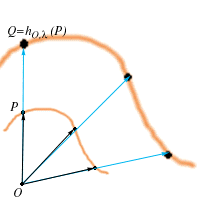 e verrà denotata con il simbolo
e verrà denotata con il simbolo
Per definizione si ha quindi
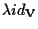 otteniamo quanto detto).
otteniamo quanto detto).
Dimostriamo che
che l'applicazione
dà un isomorfismo tra il gruppo moltiplicativo di
DIMOSTRAZIONE
- Dimostriamo che la composizione è operazione interna in
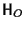 :
siano
:
siano
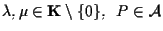 poniamo
poniamo
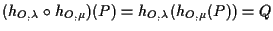 e
e
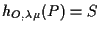 .
.
Affermiamo che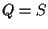 (e ciò ci permette di concludere, infatti
(e ciò ci permette di concludere, infatti
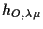 è ancora omotetia di centro
è ancora omotetia di centro 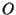 dato che
dato che
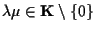 ).
).
Infatti porre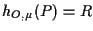 significa
significa
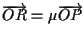 e
e
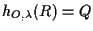 significa
significa
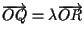 e infine
e infine
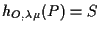 vuol dire che
vuol dire che
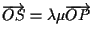 .
.
Allora otteniamo: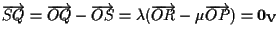 che implica
che implica 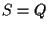 .
.
- Dimostriamo che
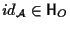 , affermiamo infatti che
, affermiamo infatti che
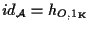 :
porre
:
porre
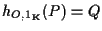 vuol dire infatti
vuol dire infatti
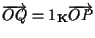 cioè
cioè 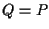 .
.
- Dimostriamo infine che l'inverso di una omotetia di centro
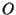 è ancora un'omotetetia di centro
è ancora un'omotetetia di centro 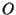 :
affermiamo che
:
affermiamo che
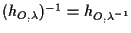 infatti porre
infatti porre
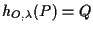 vuol dire
vuol dire
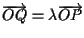 ,
per cui potremo dire che
,
per cui potremo dire che
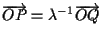 cioè proprio
cioè proprio
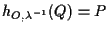 .
.
Questo conclude la dimostrazione che l'insieme delle omotetetie di centro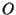 è sottogruppo di
è sottogruppo di
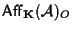 .
.
Riguardo alla seconda richiesta, le formule trovate:
è un'isomorfismo di gruppi.

 _______________
_______________
 __
__
 ________________________
________________________