|
|
31. TEOREMA
CARATTERIZZAZIONE GEOMETRICA DELLE AFFINITÀ
Sia
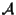 spazio affine su
spazio affine su
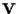 e
e
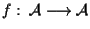 biunivoca;
biunivoca;
allora 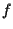 è affinità se e solo se valgono le seguenti condizioni:
è affinità se e solo se valgono le seguenti condizioni:
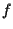 conserva il parallelismo, (nel senso quindi della terminologia già introdotta, cioè se possiede la proprietà
conserva il parallelismo, (nel senso quindi della terminologia già introdotta, cioè se possiede la proprietà 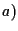 dell'osservazione 30 ),
dell'osservazione 30 ),
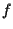 conserva il rapporto (anche qui nel senso della terminologia già introdotta).
conserva il rapporto (anche qui nel senso della terminologia già introdotta).
32. OSSERVAZIONI
I) Si noti che se
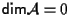 allora
allora
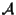 è costituito da un solo punto e l'unica applicazione di
è costituito da un solo punto e l'unica applicazione di
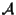 in
in
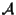 è l'identità.
è l'identità.
Se invece
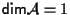 allora ogni applicazione biunivoca (cioè ogni permutazione) di
allora ogni applicazione biunivoca (cioè ogni permutazione) di
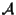 in
in
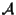 conserva il parallelismo.
conserva il parallelismo.
II) Accenniamo solamente al fatto che si può ulteriormente semplificare la definizione di "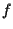 conserva il parallelismo", infatti si dimostra che se il campo base
conserva il parallelismo", infatti si dimostra che se il campo base
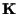 ha almeno tre elementi (cioè per ogni campo diverso da
ha almeno tre elementi (cioè per ogni campo diverso da
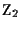 )
e quindi su una retta stanno almeno tre punti distinti, allora basta richiedere la condizione )
e quindi su una retta stanno almeno tre punti distinti, allora basta richiedere la condizione 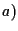 limitatamente alle rette affini (vedi SNAPPER, E., TROYER, R. J., Metric Affine Geometry, Academic Press Inc., New York, 1971).
limitatamente alle rette affini (vedi SNAPPER, E., TROYER, R. J., Metric Affine Geometry, Academic Press Inc., New York, 1971).
DIMOSTRAZIONE
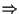 )
Il contenuto di questa implicazione risiede nelle proposizioni 16 e 19. )
Il contenuto di questa implicazione risiede nelle proposizioni 16 e 19.
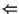 )
La dimostrazione di questa implicazione è piuttosto complessa ed è spezzata in vari passi; inoltre il caso )
La dimostrazione di questa implicazione è piuttosto complessa ed è spezzata in vari passi; inoltre il caso
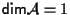 presenta qualche particolarità conseguentemente a quanto detto nell'osservazione 32 I e sarà trattato separatamente.
presenta qualche particolarità conseguentemente a quanto detto nell'osservazione 32 I e sarà trattato separatamente.
|



















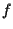 conserva il parallelismo, (nel senso quindi della terminologia già introdotta, cioè se possiede la proprietà
conserva il parallelismo, (nel senso quindi della terminologia già introdotta, cioè se possiede la proprietà 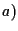 dell'osservazione 30 ),
dell'osservazione 30 ),
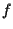 conserva il rapporto (anche qui nel senso della terminologia già introdotta).
conserva il rapporto (anche qui nel senso della terminologia già introdotta).

 _______________
_______________
 __
__
 ________________________
________________________