TEOREMA DI CARATTERIZZAZIONE GEOMETRICA DELLE AFFINITÀ

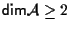
CASO $\mathsf{dim}\mathcal{A} \geq 2$

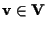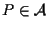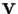
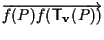I PASSO Sia $\mathbf{v} \in \mathbf{V}$ , $P \in \mathcal{A}$ ; affermiamo che il vettore di $\mathbf{V}$ $\overrightarrow{f(P)f(\mathsf{T}_{\mathbf{v}}(P))}$ non dipende da

.

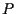Se 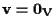$\mathbf{v}=\mathbf{0}_{\mathbf{V}}$ allora 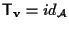$\mathsf{T}_{\mathbf{v}}=id_{\mathcal{A}}$ e quindi 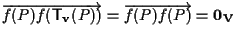$\overrightarrow{f(P)f(\mathsf{T}_{\mathbf{v}}(P))}=\overrightarrow{f(P)f(P)}=\mathbf{0}_{\mathbf{V}}$ chiaramente non dipende da

.
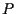Se 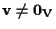$\mathbf{v}\neq\mathbf{0}_{\mathbf{V}}$ allora 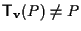$\mathsf{T}_{\mathbf{v}}(P)\neq P$ , è quindi esiste un'unica retta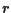

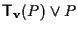, cioè $\mathsf{T}_{\mathbf{v}}(P)\vee P$ , passante per questi due punti.
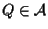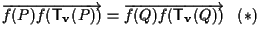Sia dunque $Q \in \mathcal{A}$ , dobbiamo provare $\overrightarrow{f(P)f(\mathsf{T}_{\mathbf{v}}(P))}=\overrightarrow{f(Q)f(\mathsf{T}_{\mathbf{v}}(Q))}\;\;\;(\ast)$ .
A questo punto distinguiamo due casi: se 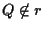$Q\not\in r$ allora i 4 punti

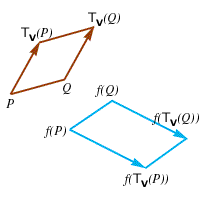
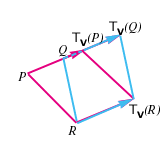
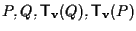$P,Q, \mathsf{T}_{\mathbf{v}}(P),\mathsf{T}_{\mathbf{v}}(Q)$ formano i vertici di un parallelogramma (segue dalle proprietà delle traslazioni) allora in virtú di esercizio 29 i punti 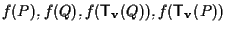$f(P),f(Q), f(\mathsf{T}_{\mathbf{v}}(P)),f(\mathsf{T}_{\mathbf{v}}(Q))$ formano un parallelogramma e quindi vale l'uguaglianza 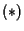$(\ast)$ grazie alla proposizione 28
Se invece $Q\in r$ ,

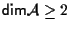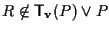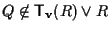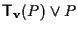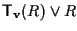poiché $\mathsf{dim}\mathcal{A} \geq 2$ , esiste certamente $R\not\in \mathsf{T}_{\mathbf{v}}(P)\vee P$ e allora vale $Q\not\in \mathsf{T}_{\mathbf{v}}(R)\vee R$ (infatti $\mathsf{T}_{\mathbf{v}}(P)\vee P$ e $\mathsf{T}_{\mathbf{v}}(R)\vee R$ sono parallele -hanno 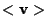$<\mathbf{v}>$ come comune giacitura- e non coincidenti e quindi disgiunte -vedi proposizione 5 della sezione "Parallelismo").
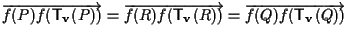Riconducendoci al caso precedente possiamo concludere $\overrightarrow{f(P)f(\mathsf{T}_{\mathbf{v}}(P))}=\overrightarrow{f(R)f(\mathsf{T}_{\mathbf{v}}(R))}=\overrightarrow{f(Q)f(\mathsf{T}_{\mathbf{v}}(Q))}$ , riottenendo cosí $(\ast)$ .

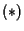Grazie a quanto visto possiamo ben definire

$\begin{displaymath}\begin{array}{cclc}\varphi:\;& \mathbf{V} & \longrightarrow &... ...overrightarrow{f(P)f(\mathsf{T}_{\mathbf{v}}(P))} \end{array}\end{displaymath}$

dove appunto nella definizione di 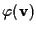$\varphi(\mathbf{v})$ possiamo utilizzare un qualsiasi punto

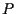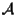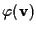di $\mathcal{A}$ che chiameremo "punto ausiliario" nel calcolo di $\varphi(\mathbf{v})$ .

______

_______________

________________________