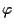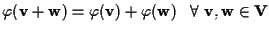
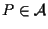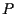II PASSO additiva: Sia ; usando come punto ausiliario nel calcolo di 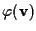e 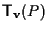come punto ausiliario nel calcolo di 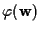potremo scriver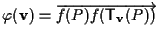e e 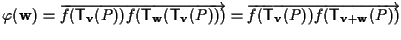. Di qui segue che 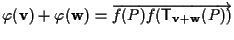avendo usato ASS.2 di spazio affine, quantità che eguaglia 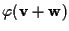: per convincersene basta calcolare questo vettore con 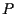come punto ausiliario. In definitiva abbiamo ottenuto che 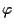è un omomorfismo del gruppo 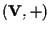su se stesso. III PASSO 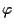iniettiva; Essendo 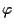un omomorfismo del gruppo 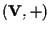su se stesso, basta dimostrare che 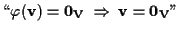. Calcoliamo 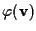con l'ausilio di un punto 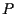: 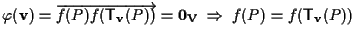; ma 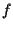è iniettiva, allora 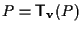e quindi (vedi esercizio 12.1 della sezione "Spazi affini: definizione e proprietà") 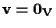. 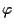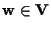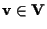IV PASSO suriettiva; Sia , vorremmo trovare tale che 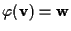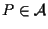. Sia e sia 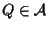tale ch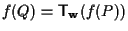e -tale 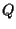certamente esiste perché 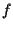è suriettiva; poniamo 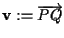e affermiamo che 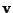fa al caso nostro: 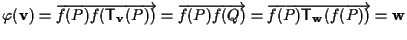ove l'ultima uguaglianza deriva dalla definizione di traslazione cosí come il fatto che 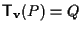. Ricapitolando, abbiamo 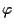additiva e biunivoca, cioè automorfismo del gruppo .
	______ _______________ __ ________________________
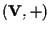