TEOREMA DI CARATTERIZZAZIONE GEOMETRICA DELLE AFFINITÀ

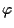V PASSO $\varphi$ porta rette in rette: se

.

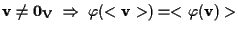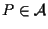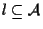Sia $P \in \mathcal{A}$ e $l\subseteq\mathcal{A}$ la retta affine passante per

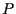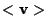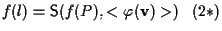e con giacitura $<\mathbf{v}>$ ; affermiamo che $f(l)=\mathsf{S}(f(P),<\varphi(\mathbf{v})>)\;\;\;(2\ast)$ .
Infatti sappiamo per ipotesi che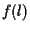

è una retta affine, ovviamente passante per

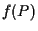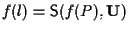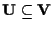e dunque potremo scrivere $f(l)=\mathsf{S}(f(P),\mathbf{U})$ ove $\mathbf{U}\subseteq\mathbf{V}$ è una retta vettoriale.
Per dimostrare $(2\ast)$ dobbiamo far vedere che $\mathbf{U}=<\varphi(\mathbf{v})>$ .
Ora si ha che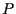

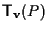e $\mathsf{T}_{\mathbf{v}}(P)$ sono distinti essendo 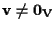$\mathbf{v}\neq\mathbf{0}_{\mathbf{V}}$ e, essendo

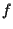iniettiva, tali resteranno

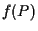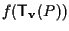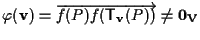e $f(\mathsf{T}_{\mathbf{v}}(P))$ per cui $\varphi(\mathbf{v})=\overrightarrow{f(P)f(\mathsf{T}_{\mathbf{v}}(P))}\neq \mathbf{0}_{\mathbf{V}}$ ; inoltre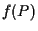

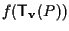e $f(\mathsf{T}_{\mathbf{v}}(P))$ stanno in

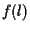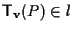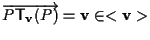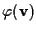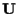(infatti $\mathsf{T}_{\mathbf{v}}(P)\in l$ perché $\overrightarrow{P\mathsf{T}_{\mathbf{v}}(P)}=\mathbf{v}\in<\mathbf{v}>$ ) e quindi $\varphi(\mathbf{v})$ starà in $\mathbf{U}$ ; trattandosi di una retta vettoriale otteniamo in definitiva proprio $(2\ast)$ .

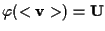Tornando alla nostra tesi primaria, ci basterà dimostrare che $\varphi(<\mathbf{v}>)=\mathbf{U}$ :
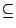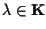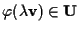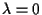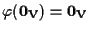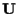$\subseteq$ ) Sia $\lambda \in \mathbf{K}$ , vorremmo che $\varphi(\lambda \mathbf{v})\in\mathbf{U}$ ; se $\lambda =0$ allora $\varphi(\mathbf{0}_{\mathbf{V}})=\mathbf{0}_{\mathbf{V}}$ che certamente sta in $\mathbf{U}$ ;
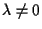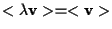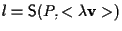se $\lambda \neq 0$ allora $<\lambda \mathbf{v}>=<\mathbf{v}>$ e quindi potremo scrivere $l=\mathsf{S}(P,<\lambda \mathbf{v}>)$ .
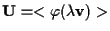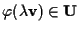Ragionando come sopra deduciamo che $\mathbf{U}=<\varphi(\lambda \mathbf{v})>$ in particolare $\varphi(\lambda \mathbf{v})\in\mathbf{U}$ .
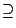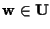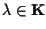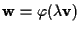$\supseteq$ ) sia $\mathbf{w}\in\mathbf{U}$ ; vorremmo trovare $\lambda \in \mathbf{K}$ tale che $\mathbf{w}=\varphi(\lambda\mathbf{v})$ ;
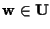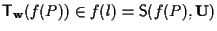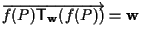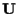ora se $\mathbf{w}\in\mathbf{U}$ allora $\mathsf{T}_{\mathbf{w}}(f(P))\in f(l)=\mathsf{S}(f(P),\mathbf{U})$ infatti $\overrightarrow{f(P)\mathsf{T}_{\mathbf{w}}(f(P))}=\mathbf{w}$ (che appunto sta in $\mathbf{U}$ ).
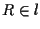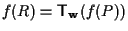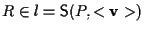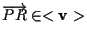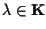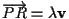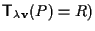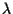Quindi esiste $R\in l$ tale che $f(R)=\mathsf{T}_{\mathbf{w}}(f(P))$ ; osserviamo che $R\in l =\mathsf{S}(P,<\mathbf{v}>)$ significa che $\overrightarrow{PR}\in <\mathbf{v}>$ cioè che esiste $\lambda \in \mathbf{K}$ tale che $\overrightarrow{PR}=\lambda\mathbf{v}$ (cioè $\mathsf{T}_{\lambda\mathbf{v}}(P)=R)$ ; affermiamo che $\lambda$ fa al caso nostro cioè 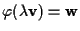$\varphi(\lambda\mathbf{v})=\mathbf{w}$ , infatti
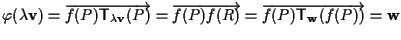$\varphi(\lambda\mathbf{v})=\overrightarrow{f(P)\mathsf{T}_{\lambda\mathbf{v}}(P... ...htarrow{f(P)f(R)}=\overrightarrow{f(P)\mathsf{T}_{\mathbf{w}}(f(P))}=\mathbf{w}$ .

VI PASSO 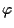$\varphi$ porta coppie di vettori linearmente indipendenti in coppie di vettori linearmente indipendenti:

.

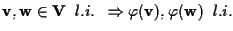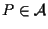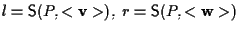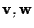Sia $P \in \mathcal{A}$ , consideriamo le rette affini $l=\mathsf{S}(P,<\mathbf{v}>),\; r=\mathsf{S}(P,<\mathbf{w}>)$ ; essendo $\mathbf{v}, \mathbf{w}$ indipendenti si ha che 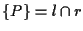$\{P\}=l\cap r$ ; di qui, essendo

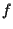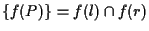iniettiva, segue che $\{f(P)\}=f(l)\cap f(r)$ .
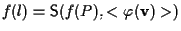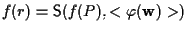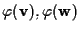Da passo V sappiamo che $f(l)=\mathsf{S}(f(P),<\varphi(\mathbf{v})>)$ e $f(r)=\mathsf{S}(f(P),<\varphi(\mathbf{w})>)$ , da cui necessariamente scende che $\varphi(\mathbf{v}), \varphi(\mathbf{w})$ sono linearmente indipendenti (si noti che si usa il fatto che su una retta affine stanno sempre almeno due punti).

______

_______________

________________________