TEOREMA DI CARATTERIZZAZIONE GEOMETRICA DELLE AFFINITÀ

VII PASSO Esiste $\mu:\;\mathbf{K}\longrightarrow\mathbf{K}$ tale che:
$\varphi(\lambda\mathbf{v})=\mu(\lambda)\varphi(\mathbf{v})\;\;\;\;\forall\; \lambda\in\mathbf{K}\;,\;\forall\;\mathbf{v}\in\mathbf{V}$ .

Sia $\mathbf{v} \in \mathbf{V},\;\mathbf{v}\neq\mathbf{0}_{\mathbf{V}}$ ; da passo V sappiamo che $\varphi(<\mathbf{v}>)=<\varphi(\mathbf{v})>$ per cui, dato $\lambda \in \mathbf{K}$ , potremo dire che $\varphi(\lambda\mathbf{v})\in<\varphi(\mathbf{v})>$ , esiste cioè $\mu_{\mathbf{v}}(\lambda)\in\mathbf{K}$ tale che $\varphi(\lambda\mathbf{v})=\mu_{\mathbf{v}}(\lambda)\varphi(\mathbf{v})$ .
Dimostriamo che lo scalare $\mu_{\mathbf{v}}(\lambda)\in\mathbf{K}$ non dipende da $\mathbf{v}$ , cioè che se $\mathbf{v}, \mathbf{w} \in \mathbf{V},\;\mathbf{v}, \mathbf{w}\neq\mathbf{0}_{\mathbf{V}}$ allora $\mu_{\mathbf{v}}(\lambda)=\mu_{\mathbf{w}}(\lambda)$ , cosicché è ben definita la funzione $\mu$ dell'enunciato.

CASO 1 $\mathbf{v}, \mathbf{w}$ linearmente indipendenti.
In particolare avremo che $\mathbf{v}+ \mathbf{w}\neq\mathbf{0}_{\mathbf{V}}$ e potremo scrivere $\varphi(\lambda(\mathbf{v}+\mathbf{w}))=\mu_{\mathbf{v}+\mathbf{w}}(\lambda)\va... ...da)\varphi(\mathbf{ v})+\mu_{\mathbf{v}+\mathbf{w}}(\lambda)\varphi(\mathbf{w})$ ove nell'ultimo passaggio abbiamo sfruttato l'additività di $\varphi$ .
D'altra parte il primo membro può essere calcolato anche svolgendo l'argomento di $\varphi$ ; sfruttando ancora passo II (cioè l'additività di 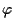) otteniamo:
$\varphi(\lambda\mathbf{v}+\lambda\mathbf{w})=\varphi(\lambda\mathbf{v})+\varphi... ...f{v}}(\lambda)\varphi(\mathbf{v})+\mu_{\mathbf{w} }(\lambda)\varphi(\mathbf{w})$ .
Sottraendo otteniamo:
$(\mu_{\mathbf{v}}(\lambda)-\mu_{\mathbf{v}+\mathbf{w}}(\lambda))\varphi(\mathbf... ...mu_{\mathbf{v}+\mathbf{w}}(\lambda))\varphi(\mathbf{w})=\mathbf{0}_{\mathbf{V}}$ .
Ma per ipotesi $\mathbf{v}, \mathbf{w}$ sono linearmente indipendenti e per passo VI lo sono anche $\varphi(\mathbf{v}), \varphi(\mathbf{w})$ e ciò implica
$\mu_{\mathbf{v}}(\lambda)=\mu_{\mathbf{w}}(\lambda)=\mu_{\mathbf{v}+\mathbf{w}} (\lambda)$ .

CASO 2 $\mathbf{v}, \mathbf{w}$ linearmente dipendenti.
Poiché $\mathsf{dim}\mathbf{V}\geq 2$ potremo certamente trovare $\mathbf{z} \in \mathbf{V}$ tale che $\mathbf{z}\not\in <\mathbf{v}>$ : per cui $\mathbf{v},\mathbf{z}$ e $\mathbf{w},\mathbf{z}$ saranno coppie di vettori linearmente indipendenti e applicando CASO 1 concludiamo per transitività.

______

_______________

________________________