TEOREMA DI CARATTERIZZAZIONE GEOMETRICA DELLE AFFINITÀ

VIII PASSO Definizione di

.
Sia $O \in \mathcal{A}$ , definiamo

$\begin{displaymath}\begin{array}{cclc} g: &\mathcal{A} & \longrightarrow & \mat... ...ightarrow{\mbox{\scriptsize {\textit{OP}}}})}(O) \end{array}\end{displaymath}$

Affermiamo che

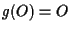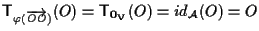infatti $\mathsf{T}_{\varphi(\overrightarrow{\mbox{\scriptsize {\textit{OO}}}})}(O)=\mathsf{T}_{\mathbf{0}_{\mathbf{V}}}(O)=id_{\mathcal{A}}(O)=O$ .
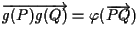
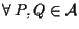$\overrightarrow{g(P)g(Q)}=\varphi(\overrightarrow{PQ})$ $\forall\;P,Q\in\mathcal{A}$ , infatti 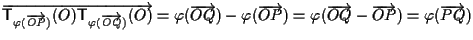$\overrightarrow{\mathsf{T}_{\varphi(\overrightarrow{\mbox{\scriptsize {\textit{... ...)=\varphi(\overrightarrow{OQ}-\overrightarrow{OP})=\varphi(\overrightarrow{PQ})$ ove si è usata l'additività di 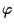$\varphi$ (che implica anche 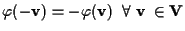$\varphi(-\mathbf{v})=-\varphi(\mathbf{v})\;\;\forall\;\mathbf{v}\;\in\mathbf{V}$ ) e l'esercizio 12.6 della sezione "Spazi affini: definizione e proprietà" per quel che concerne la prima uguaglianza.
Attenzione: con ciò non abbiamo dimostrato che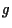 è un'affinità di 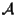$\mathcal{A}$ poiché non sappiamo (ancora) che 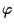$\varphi$ è lineare.
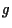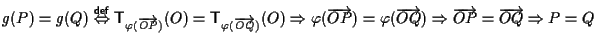
iniettiva: $g(P)=g(Q)\stackrel{\mathsf{def}}{\Leftrightarrow}\mathsf{T}_{\varphi(\overright... ...ightarrow{OQ})\Rightarrow\overrightarrow{OP}=\overrightarrow{OQ}\Rightarrow P=Q$
Se 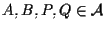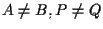$A,B,P,Q \in \mathcal{A}$ , $A\neq B,P \neq Q$ e i segmenti orientati 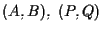$(A,B),\;(P,Q)$ sono paralleli allora anche 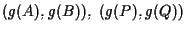$(g(A),g(B)),\;(g(P),g(Q))$ sono segmenti orientati paralleli e vale:

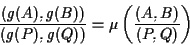
$\begin{displaymath}\frac{(g(A),g(B))}{(g(P),g(Q))}=\mu\left(\frac{(A,B)}{(P,Q)}\right) \end{displaymath}$

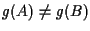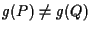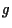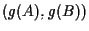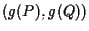Certamente $g(A)\neq g(B)$ e $g(P)\neq g(Q)$ perché è iniettiva e quindi ha senso considerare i segmenti orientati e . Dimostriamo che si tratta di segmenti paralleli e troviamone il rapporto (si ricordino le nozioni di segmenti orientati paralleli e rapporto precedentemente introdotte):
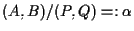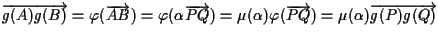posto $(A,B)/(P,Q)=:\alpha$ , abbiamo che $\overrightarrow{g(A)g(B)}=\varphi(\overrightarrow{AB})=\varphi(\alpha\overright... ...})=\mu(\alpha)\varphi(\overrightarrow{PQ})=\mu(\alpha)\overrightarrow{g(P)g(Q)}$ .

______

_______________

________________________