

 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

|

|
13. DEFINIZIONE Sia
Nel piano o nello spazio ordinario (che sono spazi affini reali) usualmente si pensa al segmento di estremi
(Esso può venir definito nel momento in cui il campo
Siano
14. DEFINIZIONE Siano
Dati due segmenti orientati
15. DEFINIZIONE Siano
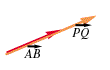
Tale scalare è detto rapporto dei segmenti orientati
Il significato di
- il segno di
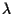 ci indica se i vettori applicati
ci indica se i vettori applicati 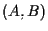 e
e 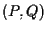 sono concordi o discordi:
sono concordi o discordi:
-
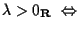
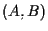 e
e 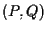 hanno lo stesso verso;
hanno lo stesso verso;
-
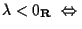
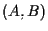 e
e 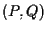 non hanno lo stesso verso;
non hanno lo stesso verso;
-
- il modulo di
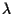 rappresenta il rapporto tra la lunghezza del segmento
rappresenta il rapporto tra la lunghezza del segmento 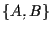 (che nel piano ordinario è indicato semplicemente con il simbolo
(che nel piano ordinario è indicato semplicemente con il simbolo 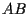 mentre la sua misura è indicata con il simbolo
mentre la sua misura è indicata con il simbolo
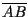 )
rispetto alla lunghezza di
)
rispetto alla lunghezza di 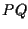 ,
o, in altre parole, la lunghezza di
,
o, in altre parole, la lunghezza di 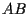 quando misurata con la lunghezza di
quando misurata con la lunghezza di 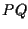 come unità di misura.
come unità di misura.
In uno spazio affine astratto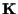 è un campo generico e non abbiamo piú la nozione di segno e modulo di
è un campo generico e non abbiamo piú la nozione di segno e modulo di 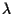 ,
ciononostante si può ancora affermare che possiamo confrontare la lunghezza di segmenti orientati paralleli, intendendo con ciò che possiamo semplicemente determinare il loro rapporto.
,
ciononostante si può ancora affermare che possiamo confrontare la lunghezza di segmenti orientati paralleli, intendendo con ciò che possiamo semplicemente determinare il loro rapporto.
Si noti che quando abbiamo costruito lo spazio dei vettori liberi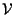 associato al piano ordinario noi non ci siamo mai serviti della possibilità di confrontare lunghezze di segmenti arbitrari (capacità che intuitivamente abbiamo nel piano ordinario e che ci permette di scegliere un segmento come unità assoluta di misura) né ci siamo serviti della possibilità di confrontare il verso di vettori applicati paralleli ma solo di confrontare la lunghezza e contemporaneamente il verso di segmenti orientati paralleli (ad esempio nel caso degenere della somma di due vettori applicati o nella definizione di moltiplicazione di un vettore applicato per un numero reale ed ancora nella definizione di vettori equipollenti).
associato al piano ordinario noi non ci siamo mai serviti della possibilità di confrontare lunghezze di segmenti arbitrari (capacità che intuitivamente abbiamo nel piano ordinario e che ci permette di scegliere un segmento come unità assoluta di misura) né ci siamo serviti della possibilità di confrontare il verso di vettori applicati paralleli ma solo di confrontare la lunghezza e contemporaneamente il verso di segmenti orientati paralleli (ad esempio nel caso degenere della somma di due vettori applicati o nella definizione di moltiplicazione di un vettore applicato per un numero reale ed ancora nella definizione di vettori equipollenti).
La stessa abilità ritroviamo ora in uno spazio affine astratto, com'era d'altra parte lecito aspettarsi.

 _______________
_______________
 __
__
 ________________________
________________________