|
|
16. PROPOSIZIONE
Sia
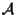 spazio affine su
spazio affine su
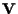 e
e
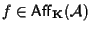 ;
sia ;
sia
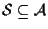 sottospazio affine di dimensione
sottospazio affine di dimensione 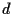 ,
allora ,
allora
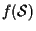 è sottospazio affine di dimensione
è sottospazio affine di dimensione 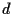 . .
"Essere sottospazio affine di dimensione 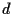 " è quindi una proprietà affine. " è quindi una proprietà affine.
DIMOSTRAZIONE
Sia
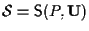 ;
sappiamo già (vedi proposizione 9) che ;
sappiamo già (vedi proposizione 9) che
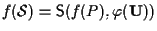 ove
ove 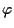 è la parte lineare di
è la parte lineare di 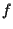 . .
Siccome 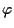 è automorfismo di
è automorfismo di
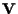 vale
vale
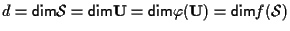 . .
17. PROPOSIZIONE
Sia
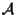 spazio affine su
spazio affine su
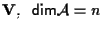 e
e
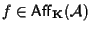 ;
siano ;
siano
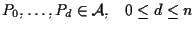 punti indipendenti.
punti indipendenti.
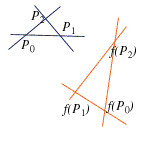
Allora
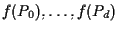 sono punti indipendenti.
sono punti indipendenti.
"Essere 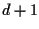 punti indipendenti" è quindi una proprietà affine.
punti indipendenti" è quindi una proprietà affine.
DIMOSTRAZIONE
Si può dimostrare osservando che
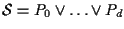 e
e
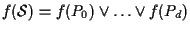 per esercizio 10.2, sottospazio che ha ancora dimensione
per esercizio 10.2, sottospazio che ha ancora dimensione 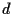 per la proposizione 16 per cui necessariamente
per la proposizione 16 per cui necessariamente
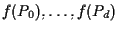 sono indipendenti.
sono indipendenti.
18. OSSERVAZIONE
Anche per le sole applicazioni affini 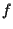 sappiamo che
sappiamo che
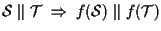 (vedi proposizione 11) per cui anche "essere sottospazi paralleli" è proprietà affine.
(vedi proposizione 11) per cui anche "essere sottospazi paralleli" è proprietà affine.
19. PROPOSIZIONE
Sia
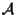 spazio affine su
spazio affine su
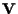 e
e
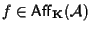 ;
sia ;
sia 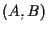 e
e 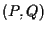 segmenti orientati paralleli (vedi definizioni 14 e 15).
segmenti orientati paralleli (vedi definizioni 14 e 15).
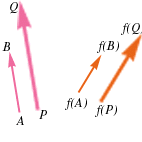
Allora
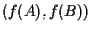 e
e
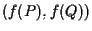 sono segmenti orientati paralleli e vale
sono segmenti orientati paralleli e vale
"Essere segmenti orientati paralleli ed avere un dato rapporto" è proprietà affine.
DIMOSTRAZIONE
Siccome 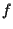 è iniettiva avremo ancora che
è iniettiva avremo ancora che
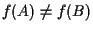 e
e
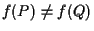 per cui ha senso considerare i segmenti orientati dell'enunciato; essi sono paralleli grazie al risultato dell'osservazione 18.
per cui ha senso considerare i segmenti orientati dell'enunciato; essi sono paralleli grazie al risultato dell'osservazione 18.
Poniamo
e
cioè
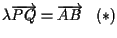 e
e
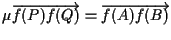 (vedi definizione 15). (vedi definizione 15).
Ma
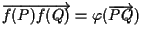 e
e
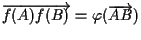 per cui:
per cui:
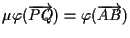 . .
Applicando 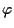 alla uguaglianza
alla uguaglianza 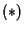 e ricordando che è lineare, in particolare omogenea, otteniamo:
e ricordando che è lineare, in particolare omogenea, otteniamo:
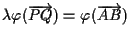 . .
Sottraendo queste due uguaglianze otteniamo
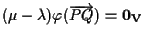 che implica
che implica
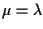 dagli assiomi di spazio vettoriale, infatti
dagli assiomi di spazio vettoriale, infatti
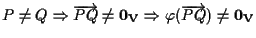 perchè
perchè 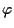 è iniettiva.
è iniettiva.
20. ESERCIZI
L'esercizio proposto è un semplice corollario della proposizione 17.

|























 _______________
_______________
 __
__
 ________________________
________________________