Mostriamo ora alcune immagini dei bacini di attrazione; mantenendo fissi i parametri e facendo diminuire l'attrito, ed ingrandendo una parte di uno dei bacini:
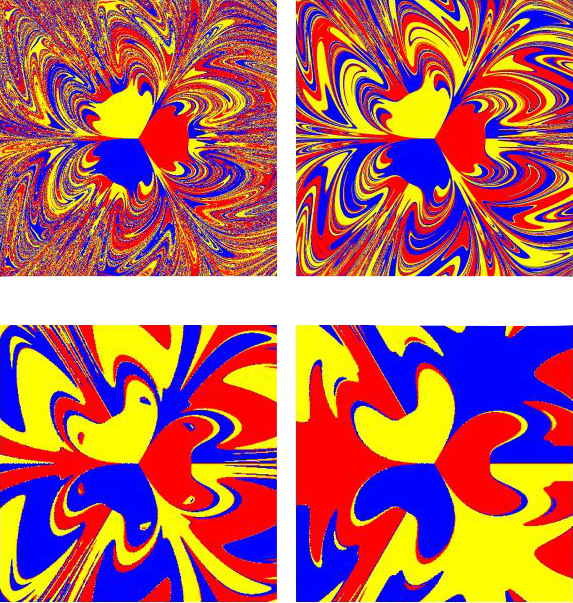

Si possono ricavare interessanti conclusioni, di cui le piú importanti (per il nostro argomento soprattutto la terza) sono:
1) I tre bacini di attrazione ricoprono tutto il piano e, se l'origine é un attrattore, sono connessi.
2) La frontiera di ogni bacino ha una forma molto complicata che permane anche supponendo nulla la forza di gravitá.
3) I bacini hanno una struttura frattale che diventa piú complessa, all'abbassarsi del coefficiente di attrito; ad ingrandimenti successivi si vede infatti
che tra due bacini, c'é sempre il terzo.
La proprietá di Wada, nel caso di un sistema caotico, si verifica quando tre o piú bacini di attrazione, hanno proprietá frattali e
condividono la stessa frontiera; nel caso particolare del pendolo magnetico vale il seguente teorema:
Teorema 2.10.
Siano i bacini di attrazione B1, B2, B3 degli equilibri asintoticamente
stabili q1, q2, q3 degli aperti del piano e lo riempiano tutto a meno di una
regione di misura nulla. Sia inoltre l'origine instabile e, per ogni x ∈ Bi e per ogni
y ∈ Bj , il segmento [x, y] contenga sempre dei punti di Bk, essendo la terna (i, j, k)
una qualsiasi permutazione di (1, 2, 3). Allora B1, B2, B3 sono dei bacini di Wada
relativi all'insieme di bacini {B1, B2, B3}.
Queste conclusioni si applicano solo a bacini bidimensionali, in quanto, ad oggi, non Ŕ ancora stata dimostrata la proprietÓ di Wada per bacini completi
del pendolo magnetico.



