|
|
X PASSO 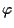 lineare:
lineare:
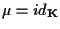 : :
Siano
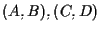 segmenti orientati paralleli; per ipotesi "
segmenti orientati paralleli; per ipotesi "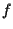 conserva il rapporto" cioè
conserva il rapporto" cioè
Posto
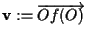 abbiamo visto che
abbiamo visto che
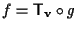 ,
quindi vale: ,
quindi vale:
avendo usato quanto stabilito in passo VIII per l'ultima uguaglianza e il fatto che
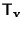 è affinità e quindi "conserva il rapporto" nell'uguaglianza precedente.
è affinità e quindi "conserva il rapporto" nell'uguaglianza precedente.
Quindi
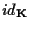 e
e 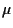 coincidono su tutti gli scalari che si possono vedere come rapporto di segmenti (orientati paralleli), cioè su tutti gli scalari non nulli. Inoltre
coincidono su tutti gli scalari che si possono vedere come rapporto di segmenti (orientati paralleli), cioè su tutti gli scalari non nulli. Inoltre
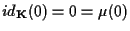 e quindi
e quindi
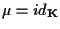 . .
CONCLUSIONI Essendo 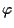 omogenea otteniamo in definitiva che
omogenea otteniamo in definitiva che 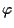 è un automorfismo dello spazio vettoriale
è un automorfismo dello spazio vettoriale
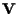 e ricordando ancora passo VIII possiamo affermare che
e ricordando ancora passo VIII possiamo affermare che 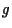 è un'affinità che fissa il punto
è un'affinità che fissa il punto 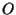 : :
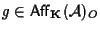 e quindi
e quindi 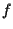 ,
che eravamo riusciuti a scrivere come ,
che eravamo riusciuti a scrivere come
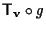 è a sua volta un'affinità come composizione di affinità.
è a sua volta un'affinità come composizione di affinità.
Si noti che si è ritrovata la "scomposizione" di un'affinità 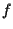 già vista in teorema 26.
già vista in teorema 26.
Si osservi che, con la sola ipotesi "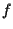 (biunivoca) conserva il parallelismo" siamo riusciti a dimostrare che esiste
(biunivoca) conserva il parallelismo" siamo riusciti a dimostrare che esiste
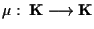 tale che
tale che
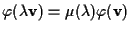
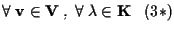 .
In realtà si può dimostrare (senza bisogno di altre ipotesi!) che .
In realtà si può dimostrare (senza bisogno di altre ipotesi!) che 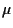 è un automorfismo del campo
è un automorfismo del campo
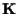 -si veda SNAPPER, E., TROYER, R. J., Metric Affine Geometry,
Academic Press Inc., New York, 1971;
applicazioni tra spazi vettoriali (sullo stesso campo base) per cui valga, come per -si veda SNAPPER, E., TROYER, R. J., Metric Affine Geometry,
Academic Press Inc., New York, 1971;
applicazioni tra spazi vettoriali (sullo stesso campo base) per cui valga, come per 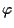 ,
la ,
la  sono dette semilineari (rispetto all'automorfismo
sono dette semilineari (rispetto all'automorfismo 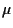 )
e un'applicazione tra spazi affini per cui valga )
e un'applicazione tra spazi affini per cui valga
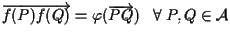 con
con 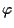 semilineare è detta semiaffine.
semilineare è detta semiaffine.
In definitiva si ottiene che un'applicazione biunica su
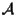 che conserva il parallelismo è un'applicazione semiaffine (tutto ciò nell'ipotesi, ricordiamolo,
che conserva il parallelismo è un'applicazione semiaffine (tutto ciò nell'ipotesi, ricordiamolo,
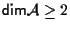 ). ).
|




















 _______________
_______________
 __
__
 ________________________
________________________