|
|
CASO
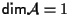
Abbiamo cioè una retta affine
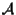 e
e 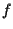 è una permutazione di
è una permutazione di
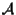 che "conserva i rapporti"; vorremmo
che "conserva i rapporti"; vorremmo 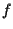 affinità, cioè trovare
affinità, cioè trovare 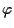 automorfismo di
automorfismo di
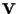 tale che
tale che
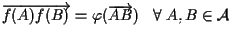 . .
Se un tale 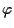 esiste, siccome esiste, siccome
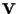 è una retta vettoriale, necessariamente, è noto dall'algebra lineare, esiste
è una retta vettoriale, necessariamente, è noto dall'algebra lineare, esiste
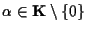 tale che
tale che
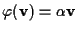 ;
dobbiamo quindi dimostrare che esiste ;
dobbiamo quindi dimostrare che esiste
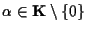 tale che
tale che
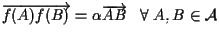 . .
Chiaramente se 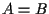 non c'è nulla da dimostrare; possiamo quindi assumere che sia
non c'è nulla da dimostrare; possiamo quindi assumere che sia 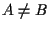 . .
Poiché
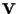 è una retta vettoriale necessariamente esiste
è una retta vettoriale necessariamente esiste
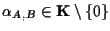 tale che
tale che
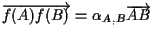 ;
dobbiamo quindi dimostrare che ;
dobbiamo quindi dimostrare che
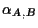 non dipende in realtà dai punti
non dipende in realtà dai punti 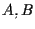 .
Consideriamo allo scopo una seconda coppia di punti distinti .
Consideriamo allo scopo una seconda coppia di punti distinti 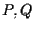 :
si tratta di dimostrare che :
si tratta di dimostrare che
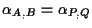 . .
Sempre dal fatto che
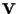 è una retta vettoriale discende che esiste
è una retta vettoriale discende che esiste
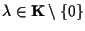 (dipendente da
(dipendente da 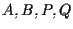 )
tale che )
tale che
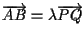 ;
sfruttiamo finalmente l'ipotesi " ;
sfruttiamo finalmente l'ipotesi "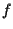 conserva i rapporti": in virtú di ciò otteniamo
conserva i rapporti": in virtú di ciò otteniamo
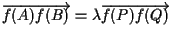 e definitiva possiamo scrivere:
e definitiva possiamo scrivere:
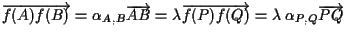
Confrontando le uguaglianze
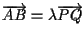 e
e
otteniamo proprio
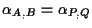 . .
|



















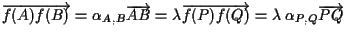

 _______________
_______________
 __
__
 ___
___