|
|
In questa sezione verranno introdotti i concetti di riferimento e coordinate che permettono di ricondurre lo studio di uno spazio affine astratto
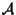 di dimensione
di dimensione 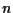 su un
su un
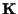 -spazio vettoriale a quello di -spazio vettoriale a quello di
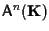 , lo spazio affine numerico su , lo spazio affine numerico su 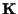 .
In sostanza effettueremo lo stesso passaggio che viene fatto nelle scuole superiori quando si inizia lo studio dello geometria analitica: fissare un'origine, due assi e due unità di misura su di essi e ricondurre lo studio del piano ordinario a quello di .
In sostanza effettueremo lo stesso passaggio che viene fatto nelle scuole superiori quando si inizia lo studio dello geometria analitica: fissare un'origine, due assi e due unità di misura su di essi e ricondurre lo studio del piano ordinario a quello di
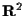 (e similmente quello dello spazio ordinario a
(e similmente quello dello spazio ordinario a
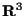 ).
Ma mentre allora bisognava necessariamente dare per scontata la corrispondenza tra i numeri reali e e i punti di una retta, ora la corrispondenza tra i punti di una retta affine di uno spazio affine ).
Ma mentre allora bisognava necessariamente dare per scontata la corrispondenza tra i numeri reali e e i punti di una retta, ora la corrispondenza tra i punti di una retta affine di uno spazio affine
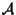 e gli elementi di
e gli elementi di
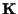 è insita nella definizione di spazio affine (e da questa corrispondenza deriva in sostanza quella tra
è insita nella definizione di spazio affine (e da questa corrispondenza deriva in sostanza quella tra
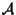 e
e
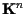 . .
|









 _______________
_______________
 __
__
 ________________________
________________________



 _______________
_______________
 __
__
 ________________________
________________________