

 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

|

|
9. PROPOSIZIONE EQUAZIONI PARAMETRICHE
Sia
- Siano
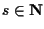 e
e
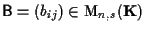 ,
,
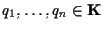 .
.
Allora l'insieme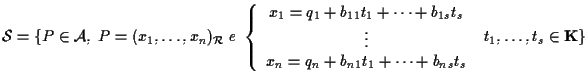
è un sottospazio affine di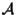 ;
precisamente vale
;
precisamente vale
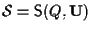 ove
ove
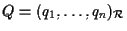 e
e
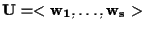 ove
ove
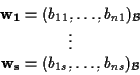
e vale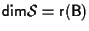 .
.
- Viceversa sia
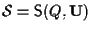 sottospazio affine di
sottospazio affine di
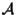 e
e
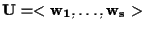 .
.
Sia
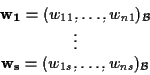
e sia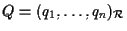 .
.
Allora se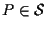 e poniamo
e poniamo
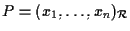 esistono
esistono
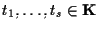 tali che
tali che
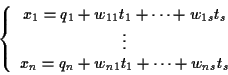
Tali espressioni sono dette equazioni parametriche
 .
.
DIMOSTRAZIONE
- Dobbiamo dimostrare che l'insieme
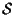 è il sottospazio affine passante per
è il sottospazio affine passante per 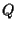 di giacitura il sottospazio vettoriale
di giacitura il sottospazio vettoriale
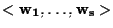 ;
sia
;
sia
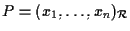 un punto di
un punto di
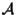 ;
si ha che
;
si ha che
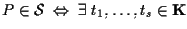 tali che
tali che
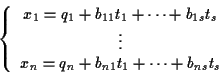
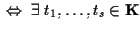 tali che
tali che
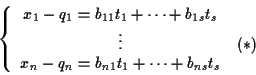
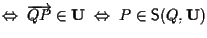 .
.
Spieghiamo come le equazioni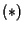 siano condizione necessaria e sufficiente affinché
siano condizione necessaria e sufficiente affinché
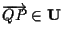 .
.
Da esercizio 2.2 sappiamo che vale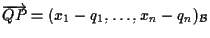 e inoltre
e inoltre
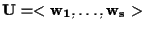 per cui
per cui
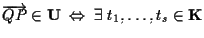 tali che
tali che
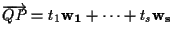 e ciò è equivalente alle equazioni
e ciò è equivalente alle equazioni 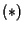 :
basta eguagliare le coordinate rispetto a
:
basta eguagliare le coordinate rispetto a
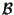 dei due membri dell'ultima eguaglianza.
dei due membri dell'ultima eguaglianza.
L'affermazione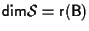 segue dal fatto che
segue dal fatto che
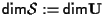 e dall'algebra lineare sappiamo che
e dall'algebra lineare sappiamo che
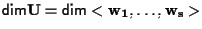 eguaglia il rango della matrice le cui colonne sono le coordinate dei vettori
eguaglia il rango della matrice le cui colonne sono le coordinate dei vettori
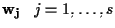 rispetto ad una qualche base di
rispetto ad una qualche base di
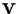 .
.
- Dall'algebra lineare sappiamo che esistono equazioni parametriche per
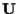 :
:
se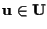 e poniamo
e poniamo
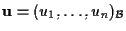 esistono
esistono
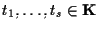 tali che
tali che
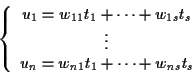
E ora sia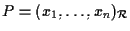 un punto di
un punto di
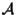 ;
si ha che ha
;
si ha che ha
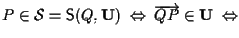
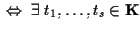 tali che
tali che
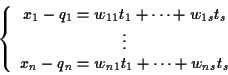
ove, ancora una volta, si è usato il fatto che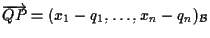 .
.

 _______________
_______________
 __
__
 ________________________
________________________