|
|
12. PROPOSIZIONE
EQUAZIONI DI UN'APPLICAZIONE AFFINE
Siano
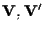

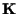 -spazi vettoriali e -spazi vettoriali e
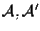 spazi affini rispettivamente su
spazi affini rispettivamente su
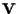 e
e
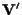 di dimensione rispettivamente
di dimensione rispettivamente 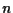 e
e 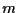 e sia
e sia
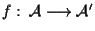 applicazione affine.
applicazione affine.
Siano
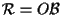 e
e
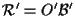 riferimenti affini rispettivamente per
riferimenti affini rispettivamente per
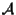 e
e
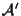 e poniamo
e poniamo
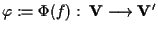 la parte lineare di
la parte lineare di 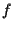 . .
Consideriamo il punto
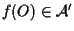 -e poniamo
-e poniamo
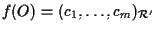 - e la matrice associata a - e la matrice associata a 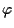 rispetto alle basi
rispetto alle basi
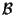 e
e
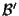
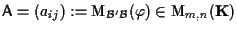 . .
Affermiamo che, se
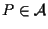 e
e
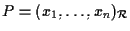 e poniamo
e poniamo 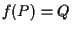 e
e
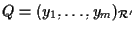 ,
allora vale ,
allora vale
o piú sinteticamente
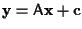 ove
ove
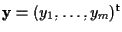 , ,
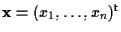 e
e
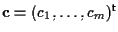 . .
Le equazioni 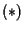 sono dette equazioni dell'applicazione
sono dette equazioni dell'applicazione 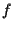 rispetto ai riferimenti
rispetto ai riferimenti
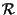 e
e
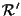 . .
DIMOSTRAZIONE
Poiché 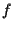 è applicazione affine si ha
è applicazione affine si ha
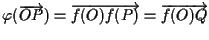 ; ;
noi dobbiamo ricercare le coordinate di 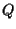 rispetto a
rispetto a
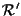 cioè le coordinate del vettore
cioè le coordinate del vettore
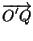 rispetto a
rispetto a
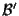 e ora si ha che
e ora si ha che
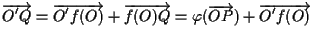 ;
per definizione di coordinate affini vale ;
per definizione di coordinate affini vale
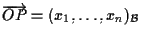 e dall'algebra lineare sappiamo che le coordinate
e dall'algebra lineare sappiamo che le coordinate
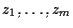 di
di
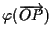 rispetto alla base
rispetto alla base
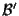 sono cosí ottenute:
sono cosí ottenute:
o piú sinteticamente
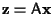 ; ;
ricordando che
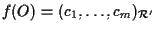 per definizione significa che le coordinate di
per definizione significa che le coordinate di
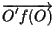 rispetto a
rispetto a
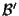 sono
sono
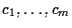 otteniamo la nostra tesi.
otteniamo la nostra tesi.
13. ESERCIZI
Gli esercizi proposti trattano casi numerici

|















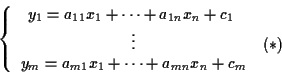
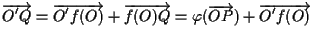 ;
per definizione di coordinate affini vale
;
per definizione di coordinate affini vale
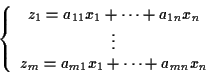
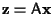 ;
;


 _______________
_______________
 __
__