CAMBIAMENTI DI COORDINATE AFFINI

6. PROPOSIZIONE CAMBIAMENTI DI COORDINATE
Sia $\mathcal{A}$ spazio affine su $\mathbf{V}$ , $\;\;$ $\mathsf{dim}\mathcal{A}=n$ e $\mathcal{R}=E\mathcal{B}$ e $\mathcal{F}=F\mathcal{C}$ due riferimenti affini per $\mathcal{A}$ .
Se $P \in \mathcal{A}$ e $P=(x_1,\ldots,x_n)_{\mathcal{R}}$ , allora $P=(y_1,\ldots,y_n)_{\mathcal{F}}$ ove

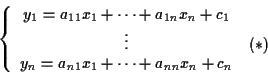
$\begin{displaymath}\left\{\begin{array}{cc} y_1=a_{11}x_1+\cdots+a_{1n}x_n+c_1 ... ...)\\ y_n=a_{n1}x_1+\cdots+a_{nn}x_n+c_n &\; \end{array}\right. \end{displaymath}$

o piú sinteticamente

ove

è la matrice di passaggio dalla base $\mathcal{B}$ alla base $\mathcal{C}$ e $c_1,\ldots,c_n$ sono le coordinate dell'origine

del riferimento $\mathcal{R}$ rispetto al riferimento $\mathcal{F}$ : $E=(c_1,\ldots,c_n)_{\mathcal{F}}$ .
Le $(\ast)$ sono dette formule del cambiamento di coordinate dal riferimento $\mathcal{R}$ al riferimento $\mathcal{F}$ .

DIMOSTRAZIONE Dobbiamo trovare le coordinate del vettore $\overrightarrow{FP}$ rispetto alla base $\mathcal{C}$ ; ora abbiamo che $\overrightarrow{FP}=\overrightarrow{FE}+\overrightarrow{EP}$ e sappiamo che $\overrightarrow{FE}=(c_1,\ldots,c_n)_{\mathcal{C}}$ e $\overrightarrow{EP}=(x_1,\ldots,x_n)_{\mathcal{B}}$ (per definizione di riferimento e coordinate affini).
Dall'algebra lineare sappiamo che

ove

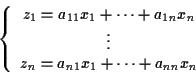
o piú sinteticamente 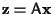$\mathbf{y}=\mathsf{A}\mathbf{x}$ , e da ciò segue la tesi.

7. ESERCIZI L'esercizio proposto tratta un caso numerico.

______

_______________

________________________