EQUAZIONI CARTESIANE

8. PROPOSIZIONE EQUAZIONI CARTESIANE
Sia $\mathcal{A}$ spazio affine su $\mathbf{V}$ , $\mathsf{dim}\mathcal{A}=n$ e sia $\mathcal{R}=O\mathcal{B}$ un riferimento affine su $\mathcal{A}$ e sia $r\in\mathbf{N}$ ; poniamo $\mathcal{B}=(\mathbf{v_1},\ldots,\mathbf{v_n})$ .

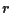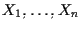
Se il sistema lineare (a coefficienti in $\mathbf{K}$ ) a equazioni e nelle incognite $X_1,\ldots,X_n$

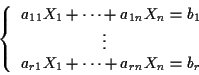
$\begin{displaymath}\left\{\begin{array}{c} a_{11}X_1+\cdots+a_{1n}X_n=b_1 \\ \vdots \;\;\; \\ a_{r1}X_1+\cdots+a_{rn}X_n=b_r \end{array} \end{displaymath}$

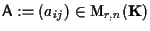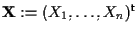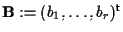-o piú sinteticamente $\mathsf{A}\mathbf{X}=\mathbf{B}$ ove $\mathsf{A}:=(a_{ij})\in\mathrm{M}_{r,n}(\mathbf{K})$ , $\mathbf{X}:=(X_1,\ldots,X_n)^{\mathsf{t}}$ e $\mathbf{B}:=(b_1,\ldots,b_r)^{\mathsf{t}}$ -
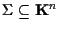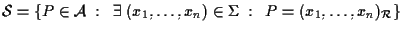è risolubile, cioè $\Sigma\subseteq\mathbf{K}^{n}$ , l'insieme delle soluzioni, è non vuoto, allora l'insieme $\mathcal{S}=\{P \in \mathcal{A}\;:\;\;\exists\;(x_1,\ldots,x_n)\in\Sigma\;:\;\;P=(x_1,\ldots,x_n)_{\mathcal{R}}\}$ è un sottospazio affine di 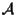$\mathcal{A}$ di giacitura 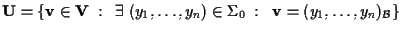$\mathbf{U}=\{\mathbf{v} \in \mathbf{V}\;:\;\;\exists\;(y_1,\ldots,y_n)\in\Sigma_0\;:\;\;\mathbf{v}=(y_1,\ldots,y_n)_{\mathcal{B}}\}$ ove $\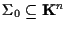Sigma_0\subseteq\mathbf{K}^n$ è l'insieme delle soluzioni del sistema omogeneo associato $\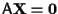mathsf{A}\mathbf{X}=\mathbf{0}$ .
Inoltre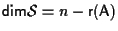 $\mathsf{dim}\mathcal{S}=n-\mathsf{r(A)}$ .
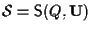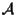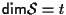Viceversa se $\mathcal{S}=\mathsf{S}(Q,\mathbf{U})$ è sottospazio affine di $\mathcal{A}$ e $\mathsf{dim}\mathcal{S}=t$ , allora possiamo trovare un sistema lineare

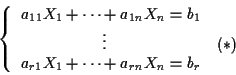
$\begin{displaymath}\left\{\begin{array}{cc} a_{11}X_1+\cdots+a_{1n}X_n=b_1 &\;\... ...; & (\ast)\\ a_{r1}X_1+\cdots+a_{rn}X_n=b_r & \; \end{array} \end{displaymath}$

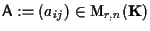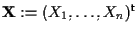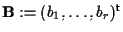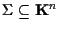-o piú sinteticamente $\mathsf{A}\mathbf{X}=\mathbf{B}$ ove $\mathsf{A}:=(a_{ij})\in\mathrm{M}_{r,n}(\mathbf{K})$ , $\mathbf{X}:=(X_1,\ldots,X_n)^{\mathsf{t}}$ e $\mathbf{B}:=(b_1,\ldots,b_r)^{\mathsf{t}}$ - risolubile, di rango e tale che, posto $\Sigma\subseteq\mathbf{K}^{n}$ l'insieme delle soluzioni del sistema, si abbia
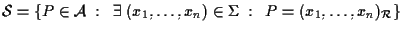$\mathcal{S}=\{P \in \mathcal{A}\;:\;\;\exists\;(x_1,\ldots,x_n)\in\Sigma\;:\;\;P=(x_1,\ldots,x_n)_{\mathcal{R}}\}$ .
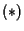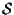Le equazioni $(\ast)$ sono dette equazioni cartesiane di $\mathcal{S}$ .
In particolare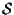 $\mathcal{S}$ può venir descritto esattamente da 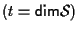$(t=\mathsf{dim}\mathcal{S})$ equazioni cartesiane.

DIMOSTRAZIONE

Innanzitutto sappiamo dall'algebra lineare che 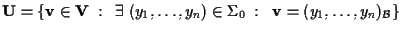$\mathbf{U}=\{\mathbf{v} \in \mathbf{V}\;:\;\;\exists\;(y_1,\ldots,y_n)\in\Sigma_0\;:\;\;\mathbf{v}=(y_1,\ldots,y_n)_{\mathcal{B}}\}$ è sottospazio vettoriale di 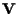$\mathbf{V}$ -si ricordi che $\Sigma_0$ non è mai vuoto.
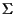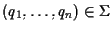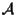
ora per ipotesi $\Sigma$ non è vuoto e sia quindi $(q_1,\ldots,q_n)\in\Sigma$ e consideriamo il punto di $\mathcal{A}$ $\;\;\;$ $Q=(q_1,\ldots,q_n)_{\mathcal{R}}$ ; per definizione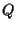

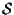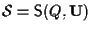appartiene all'insieme $\mathcal{S}$ ; se dimostreremo che $\mathcal{S}=\mathsf{S}(Q,\mathbf{U})$ avremo finito:
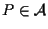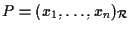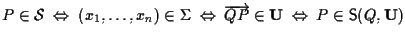sia $P \in \mathcal{A}$ e poniamo $P=(x_1,\ldots,x_n)_{\mathcal{R}}$ , allora $P \in \mathcal{S}\;\Leftrightarrow\;(x_1,\ldots,x_n)\in\Sigma\;\Leftrightarrow\;\overrightarrow{QP}\in\mathbf{U}\;\Leftrightarrow\;P\in\mathsf{S}(Q,\mathbf{U})$ .
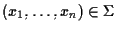Spieghiamo la penultima implicazione: noi sappiamo che $\overrightarrow{QP}=(x_1-q_1,\ldots,x_n-q_n)_{\mathcal{B}}$ (vedi esercizio 2.2) e se $(x_1,\ldots,x_n)\in\Sigma$ allora

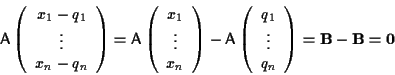
$\begin{displaymath}\mathsf{A}\left(\begin{array}{c} x_1-q_1\\ \vdots\\ x_n-q_n... ...dots\\ q_n \end{array}\right)=\mathbf{B}-\mathbf{B}=\mathbf{0}\end{displaymath}$

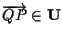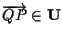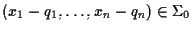cioè $\overrightarrow{QP}\in\mathbf{U}$ e viceversa se $\overrightarrow{QP}\in\mathbf{U}$ cioè $(x_1-q_1,\ldots,x_n-q_n)\in\Sigma_{0}$ allora

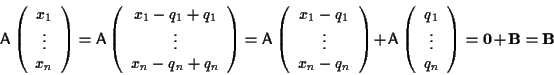
$\begin{displaymath}\mathsf{A}\left(\begin{array}{c} x_1\\ \vdots\\ x_n \end{ar... ...dots\\ q_n \end{array}\right)=\mathbf{0}+\mathbf{B}=\mathbf{B}\end{displaymath}$

cioè $(x_1,\ldots,x_n)\in\Sigma$ .
L'affermazione sulla dimensione segue da considerazioni di algebra lineare.

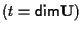
Dall'algebra lineare sappiamo che esiste un sistema lineare omogeneo di rango $(t=\mathsf{dim}\mathbf{U})$

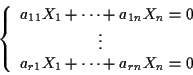
$\begin{displaymath}\left\{\begin{array}{c} a_{11}X_1+\cdots+a_{1n}X_n=0 \\ \vdots \;\;\;\\ a_{r1}X_1+\cdots+a_{rn}X_n=0 \end{array} \end{displaymath}$

tale che, posto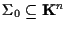 $\Sigma_0\subseteq\mathbf{K}^n$ l'insieme delle soluzioni di tale sistema, si abbia 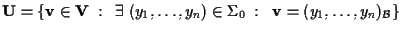$\mathbf{U}=\{\mathbf{v} \in \mathbf{V}\;:\;\;\exists\;(y_1,\ldots,y_n)\in\Sigma_0\;:\;\;\mathbf{v}=(y_1,\ldots,y_n)_{\mathcal{B}}\}$ (esistono cioè equazioni cartesiane per il sottospazio vettoriale $\mathbf{U}$ ).
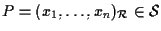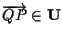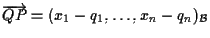Poniamo $Q=(q_1,\ldots,q_n)_{\mathcal{R}}$ e sia $P=(x_1,\ldots,x_n)_{\mathcal{R}}\in\mathcal{S}$ cioè $\overrightarrow{QP}\in\mathbf{U}$ ; d'altra parte sappiamo che $\overrightarrow{QP}=(x_1-q_1,\ldots,x_n-q_n)_{\mathcal{R}}$ e quindi deve valere

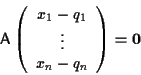
$\begin{displaymath}\mathsf{A}\left(\begin{array}{c} x_1-q_1\\ \vdots\\ x_n-q_n \end{array}\right)=\mathbf{0} \end{displaymath}$

ossia

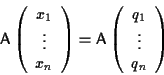
$\begin{displaymath}\mathsf{A}\left(\begin{array}{c} x_1\\ \vdots\\ x_n \end{ar... ...\left(\begin{array}{c} q_1\\ \vdots\\ q_n \end{array}\right) \end{displaymath}$

Ponendo

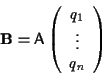
$\begin{displaymath}\mathbf{B}= \mathsf{A}\left(\begin{array}{c} q_1\\ \vdots\\ q_n \end{array}\right)\end{displaymath}$

otteniamo il sistema cercato.

______

_______________

________________________