DEFINIZIONE DI RIFERIMENTO AFFINE E DI COORDINATE

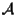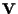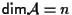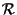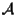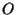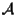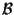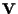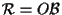1. DEFINIZIONE Sia $\mathcal{A}$ spazio affine su $\mathbf{V}$ , $\mathsf{dim}\mathcal{A}=n$ ; diciamo che assegnamo un riferimento affine $\mathcal{R}$ su $\mathcal{A}$ nel momento in cui fissiamo un punto di $\mathcal{A}$ , detto origine del riferimento, e una base $\mathcal{B}$ di $\mathbf{V}$ ; scriveremo $\mathcal{R}=O\mathcal{B}$ .

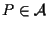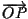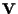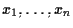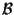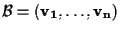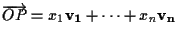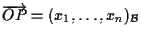Sia $P \in \mathcal{A}$ ; il vettore $\overrightarrow{OP}$ sta in $\mathbf{V}$ e avrà certe coordinate $x_1,\ldots,x_n$ rispetto a $\mathcal{B}$ (ricordiamo che se $\mathcal{B}=(\mathbf{v_1},\ldots,\mathbf{v_n})$ quanto detto significa $\overrightarrow{OP}=x_1\mathbf{v_1}+\cdots+x_n\mathbf{v_n}$ e noi scriveremo $\overrightarrow{OP}=(x_1,\ldots,x_n)_{\mathcal{B}}$ );
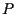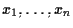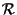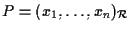diremo che ha coordinate $x_1,\ldots,x_n$ rispetto a $\mathcal{R}$ e scriveremo $P=(x_1,\ldots,x_n)_{\mathcal{R}}$ .

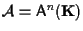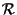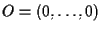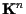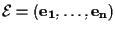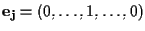Se $\mathcal{A}=\mathsf{A}^{n}(\mathbf{K})$ (vedi esempio 6 della sezione "Spazi affini: definizione e proprietà") il riferimento $\mathcal{R}$ che ha per origine il punto $O=(0,\ldots,0)$ e in cui la base di $\mathbf{K}^n$ è quella canonica: $\mathcal{E}=(\mathbf{e_1},\ldots,\mathbf{e_n})$ , in cui $\mathbf{e_j}=(0,\ldots,1,\ldots,0)$ cioè l'unica componente non nulla è quella al 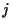-esimo posto, è detto riferimento standard.
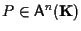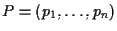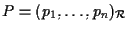Si osservi che se $P\in\mathsf{A}^{n}(\mathbf{K})$ allora $P=(p_1,\ldots,p_n)$ se e solo se $P=(p_1,\ldots,p_n)_{\mathcal{R}}$ .

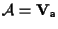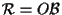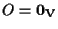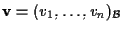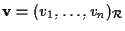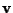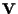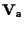Se $\mathcal{A}=\mathbf{V}_\mathsf{a}$ (vedi esempio 5 della sezione "Spazi affini: definizione e proprietà") e $\mathcal{R}=O\mathcal{B}$ è un riferimento in cui $O=\mathbf{0}_{\mathbf{V}}$ allora vale $\mathbf{v}=(v_1,\ldots,v_n)_{\mathcal{B}}$ se e solo se $\mathbf{v}=(v_1,\ldots,v_n)_{\mathcal{R}}$ in cui prima consideriamo $\mathbf{v}$ come vettore di $\mathbf{V}$ e dopo come punto di $\mathbf{V}_\mathsf{a}$ .

Si osservi come ogni punto di 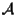$\mathcal{A}$ possieda un'unica n-pla di coordinate rispetto a 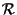$\mathcal{R}$ e viceversa come ogni n-pla di elementi di 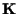$\mathbf{K}$ rappresenti le coordinate rispetto a 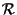$\mathcal{R}$ di un unico punto; ossia l'applicazione

$\begin{displaymath}\begin{array}{llll} \varphi_{\mathcal{R}}: & \mathcal{A} & \l... ...hbf{K}^{n} \\ \; & P & \mapsto & (x_1,\ldots,x_n) \end{array} \end{displaymath}$

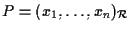ove $P=(x_1,\ldots,x_n)_{\mathcal{R}}$ , è ben definita e biunivoca.

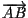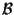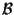2. ESERCIZI Negli esercizi, fra l'altro, si determinano le coordinate di un vettore $\overrightarrow{AB}$ rispetto ad una data base $\mathcal{B}$ , note le coordinate degli estremi rispetto ad un riferimento affine che abbia $\mathcal{B}$ come base.

______

_______________

________________________