| Introduzione |
| Gruppi di isometrie |
| Gruppo di
simmetria di una figura |
| Gruppi discreti |
| Gruppi di simmetria dei rosoni |
| Gruppi ciclici |
| Gruppi diedrali |
| Il caleidoscopio |
| Simboli |
| Bibliografia |
Vediamo un esempio di come una piccola modifica di un disegno cambi immediatamente il relativo gruppo di simmetria.
Prendiamo una tra le più semplici immagini che presentano simmetrie:
 |
questa figura viene chiamata tripoide ed ha D3 come gruppo di simmetria. |
ora se si vogliono eliminare le simmetrie di riflessione, basta aggiungere alle tre banderuole tre bracci:
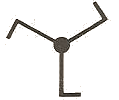 |
Si ottiene così il gruppo di simmetria C3. Questa figura si chiama triscele , è un antico simbolo magico. I greci l'hanno usato come simbolo per la Sicilia (Trinacria, isola a tre vertici), aggiungendovi al centro la testa della 'Medusa'. Inoltre il triscele è stato anche utilizzato come sigillo sulla copertina dei Rendiconti del Circolo Matematico di Palermo. |
 |
Un motivo per cui si attribuisce potere magico a simili simboli, sostiene Weyl nel suo libro La Simmetria , potrebbe risiedere proprio in questa simmetria incompleta data da rotazioni senza riflessioni.
 |

