| Introduzione |
| Gruppi di isometrie |
| Gruppo di
simmetria di una figura |
| Gruppi discreti |
| Gruppi di simmetria dei rosoni |
| Gruppi ciclici |
| Gruppi diedrali |
| Il caleidoscopio |
| Simboli |
| Bibliografia |
Vediamo invece cosa succede per i gruppi D2 e C4
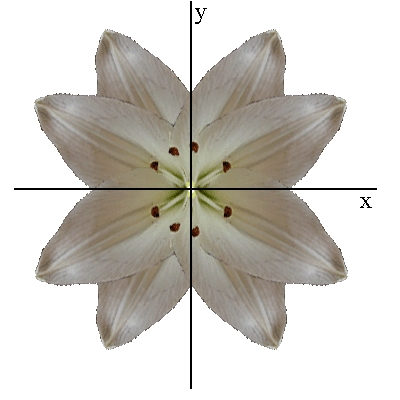 |
 |
D2 = { 1 , ρπ , rx , ry } |
C4 = { 1 , ρπ/2 , ρπ , ρ3π/2} |
Entrambi i gruppi hanno ordine 4 ma non sono isomorfi perchè le relazioni fra gli elementi sono diverse in quanto sono diversi i periodi dei generatori: D2 = < ρπ , rx > con ( ρπ )2 = ( rx )2 = 1 , invece C4 = <ρπ/2 > con (ρπ/2)4 = 1.
Quest'ultima asserzione mette in evidenza il fatto che, per dare una buona descrizione delle simmetrie di una figura F, non è sufficiente contare le isometrie che riportano F in se stessa, ma bisogna anche tenere conto delle relazioni che intercorrono fra tali isometrie, ovvero come si compongono e qual è il loro ordine.
Quindi il numero degli elementi misura la dimensione del gruppo , e il gruppo misura invece la simmetria.
 |

