| Introduzione |
| Gruppi di isometrie |
| Gruppo di
simmetria di una figura |
| Gruppi discreti |
| Gruppi di simmetria dei rosoni |
| Gruppi ciclici |
| Gruppi diedrali |
| Il caleidoscopio |
| Simboli |
| Bibliografia |
Gruppi ciclici e gruppi diedrali
Vediamo ora nello specifico alcuni gruppi ciclici ed alcuni gruppi diedrali
C1 = { 1 } indica l'assenza totale di simmetria. Infatti data F tale che Isom(F) = C1 , tale figura potrà ritornare su se stessa solo attraverso l'identità , e non si può trovare una parte più piccola del disegno che attraverso un qualche movimento rigeneri F. |
 |
|---|
D1 rappresenta invece la simmetria bilaterale, l'idea di simmetria che più o meno tutti hanno, la classica simmetria a specchio.
I suoi elementi sono { 1 , rl } quindi anche se fa parte dei gruppi diedrali è in realtà un gruppo ciclico, come C2. Hanno entrambi cardinalità 2, ma gli elementi non banali sono diversi:
 |
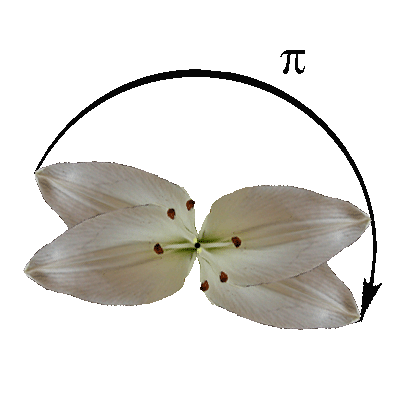 |
| D1 contiene una riflessione di asse l | C2 una rotazione di angolo π. |
D1 e C2 sono comunque isomorfi, infatti si può costruire un'isomorfismo mandando l'identità nell'identità e rl in ρθ.
Non ci sono problemi per quanto riguarda la composizione in quanto gli elementi dei due gruppi sono legati dalla stessa relazione
( rl )2 = ( ρθ )2 = 1.
 |

