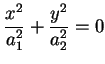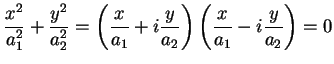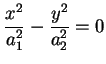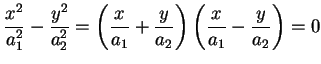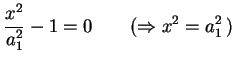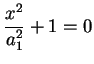Le seguenti equazioni di secondo grado sono prodotti
di equazioni di primo grado e pertanto rappresentano coppie di
piani.
La quadrica di equazione
rappresenta in campo reale solo i punti dell'asse 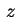 ; ma in
campo complesso si ha:
e quindi la superficie è formata dai due piani (complessi) di
equazione
La quadrica di equazione
rappresenta due piani reali non paralleli. In effetti si ha:
e quindi la superficie è formata dai due piani di equazione ; ma in
campo complesso si ha:
e quindi la superficie è formata dai due piani (complessi) di
equazione
La quadrica di equazione
rappresenta due piani reali non paralleli. In effetti si ha:
e quindi la superficie è formata dai due piani di equazione
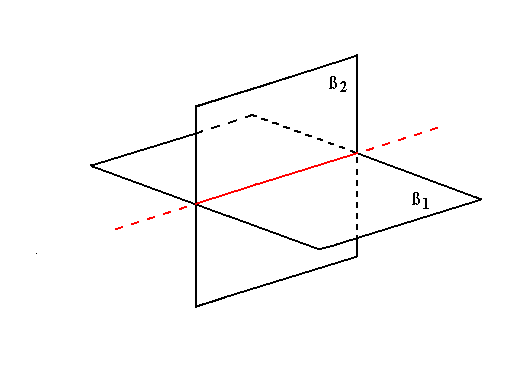
Se consideriamo, invece, l'equazione
con 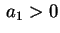 , essa rappresenta i due piani reali, distinti e
paralleli di equazioni , essa rappresenta i due piani reali, distinti e
paralleli di equazioni
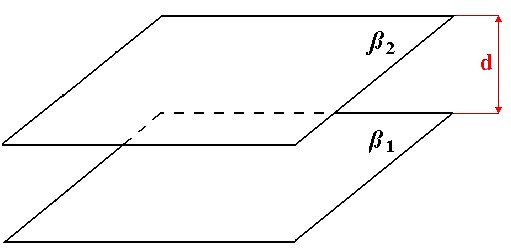
Anche l'equazione
(sempre con 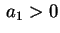 ) è suddivisibile in due piani distinti e paralleli
che, però, sono complessi coniugati.
Infine la quadrica d'equazione ) è suddivisibile in due piani distinti e paralleli
che, però, sono complessi coniugati.
Infine la quadrica d'equazione
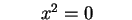 rappresenta
il piano rappresenta
il piano 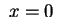 contato due volte. contato due volte.
|