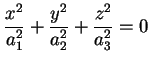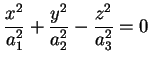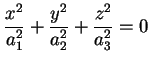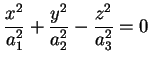Un cono 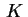 di vertice il punto di vertice il punto 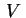 è una superficie
è una superficie 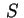 che gode della seguente proprietà:
per ogni punto che gode della seguente proprietà:
per ogni punto
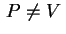 di di 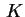 , la retta , la retta 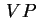 è
completamente contenuta
in è
completamente contenuta
in 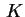 . .
Una funzione
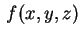 si dice omogenea di grado
k se si ha: si dice omogenea di grado
k se si ha:
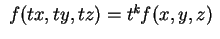 per ogni scelta di per ogni scelta di
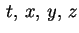 .
L'equazione .
L'equazione
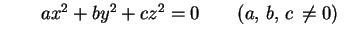 rappresenta
un cono di vertice l'origine rappresenta
un cono di vertice l'origine 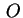 , poiché è omogenea di secondo grado. , poiché è omogenea di secondo grado.
Infatti se prendiamo un punto
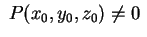 tale che tale che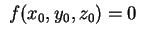 allora la retta allora la retta
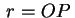 è tutta contenuta nella superficie dal momento che è tutta contenuta nella superficie dal momento che 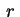 ha equazioni: ha equazioni:
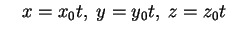 e e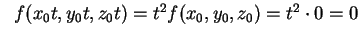 . .
Se
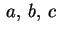 hanno lo stesso segno, in campo reale esso
è costituito dal solo punto hanno lo stesso segno, in campo reale esso
è costituito dal solo punto 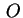 , il suo vertice. È il caso
della quadrica , il suo vertice. È il caso
della quadrica
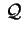 di equazione ridotta
dove di equazione ridotta
dove
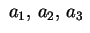 sono sono 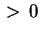 . Tale cono è anche
detto semi-immaginario. . Tale cono è anche
detto semi-immaginario.
Se consideriamo la quadrica con equazione ridotta
dove
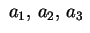 sono sono 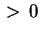 , essa rappresenta un
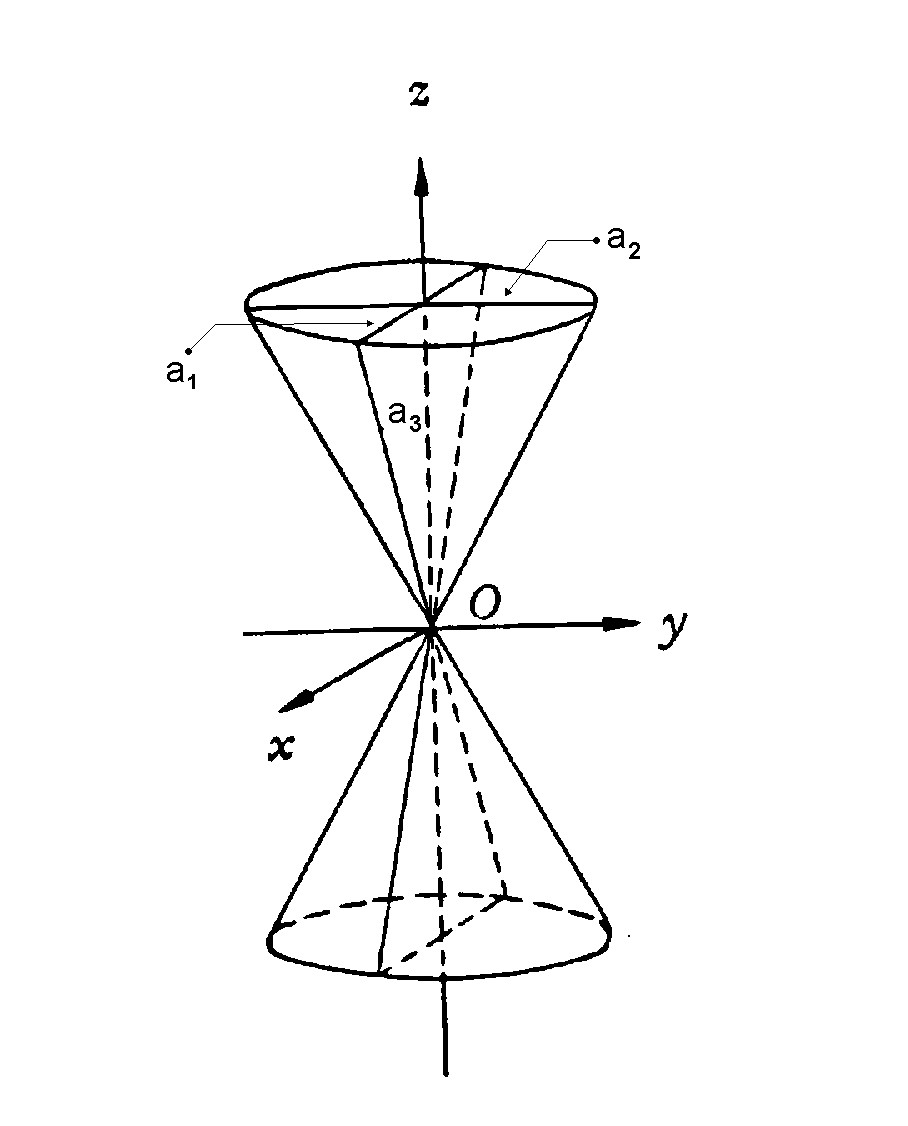
cono reale di vertice l'origine. Gli assi coordinati sono assi di
simmetria e i piani coordinati sono piani di simmetria.
Le intersezioni con i piani , essa rappresenta un
cono reale di vertice l'origine. Gli assi coordinati sono assi di
simmetria e i piani coordinati sono piani di simmetria.
Le intersezioni con i piani 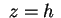 sono ellissi che diventano
sempre più grandi al crescere di sono ellissi che diventano
sempre più grandi al crescere di 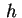 (in modulo). (in modulo).
|