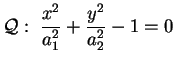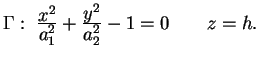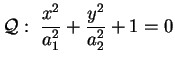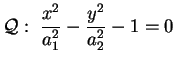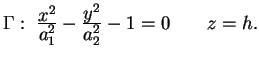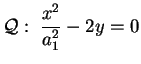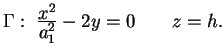Una superficie  è un cilindro se è unione di
rette tutte parallele ad una stessa retta (o ad uno stesso
vettore). Tali rette si chiamano generatrici del
cilindro. Una curva è un cilindro se è unione di
rette tutte parallele ad una stessa retta (o ad uno stesso
vettore). Tali rette si chiamano generatrici del
cilindro. Una curva
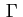 contenuta in contenuta in 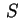 e che
incontra tutte le generatrici si chiama direttrice di e che
incontra tutte le generatrici si chiama direttrice di 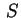 .
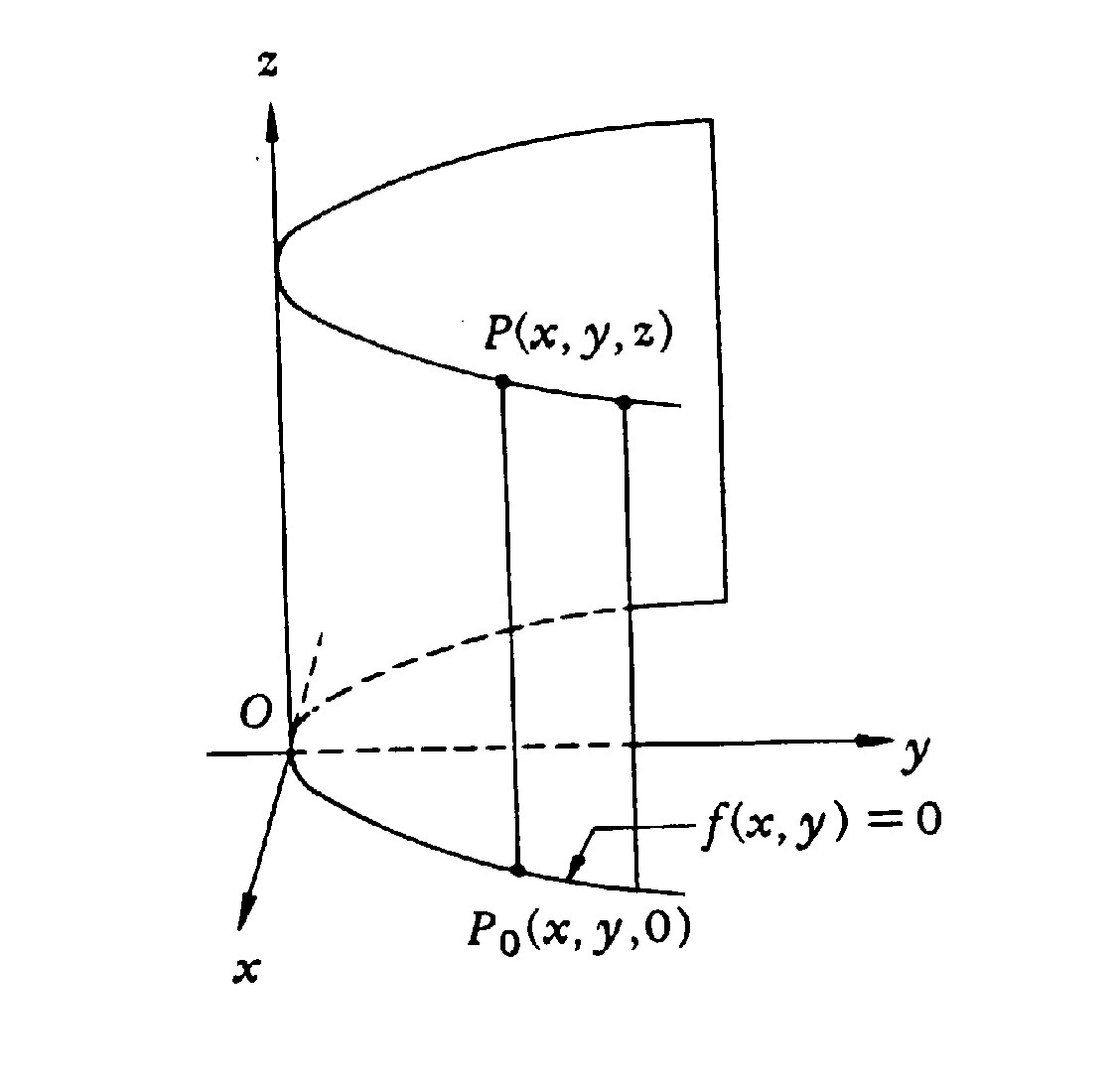
In generale un'equazione del tipo .
In generale un'equazione del tipo
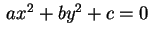 in cui non
compare la in cui non
compare la 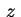 rappresenta, nello spazio, un cilindro avente
generatrici parallele all'asse rappresenta, nello spazio, un cilindro avente
generatrici parallele all'asse 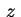 che incontrano, nel piano
che incontrano, nel piano 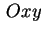 la curva di equazione la curva di equazione
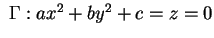 . .
Basta infatti osservare che se
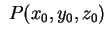 è un punto
della superficie, ciò significa che si ha è un punto
della superficie, ciò significa che si ha
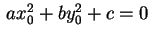 indipendentemente dal valore di indipendentemente dal valore di 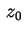 .
Pertanto ogni altro punto .
Pertanto ogni altro punto
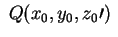 della retta
per della retta
per 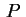 e parallela all'asse e parallela all'asse 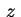 soddisfa l'equazione,
comunque si faccia variare soddisfa l'equazione,
comunque si faccia variare
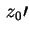 ; cioè l'intera retta
per ; cioè l'intera retta
per 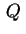 e parallela all'asse e parallela all'asse 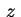 è contenuta nella
superficie.
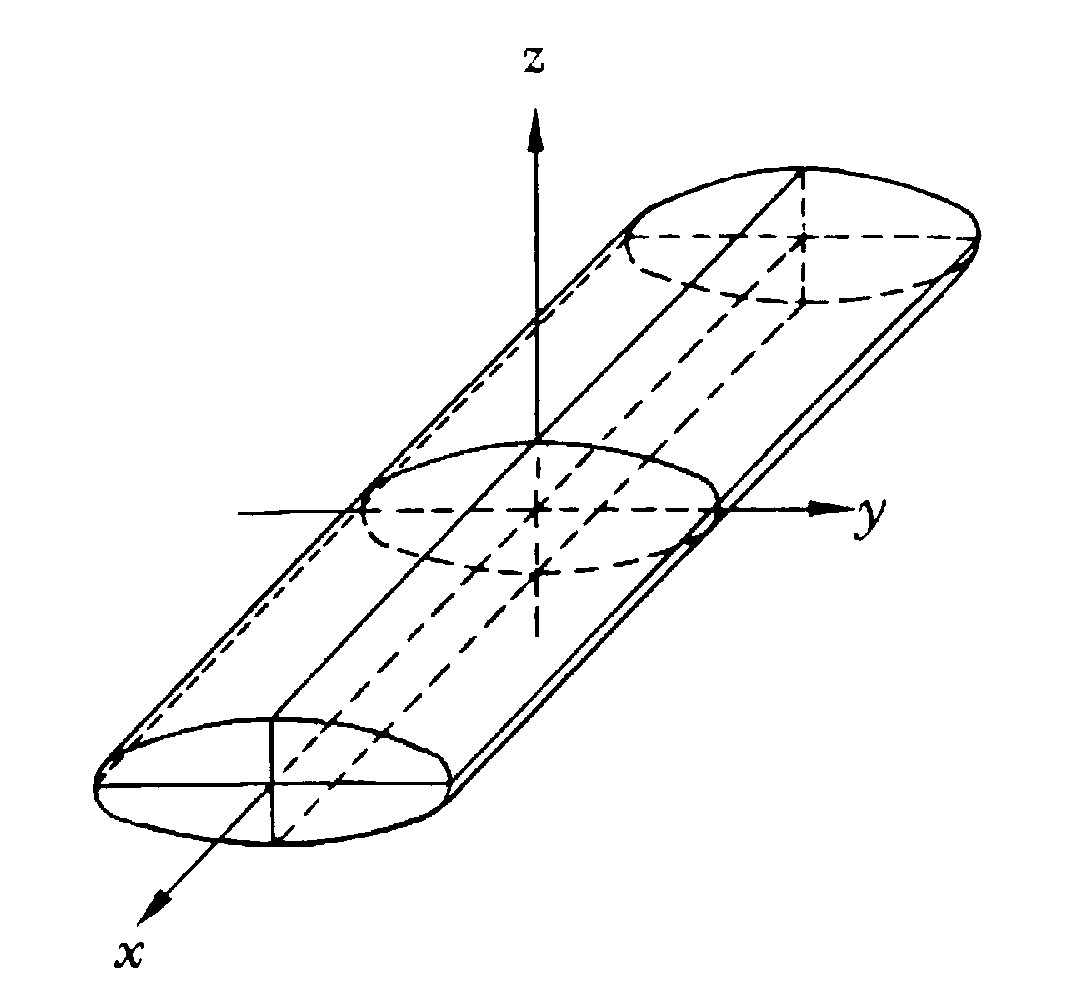
Consideriamo la quadrica di equazione ridotta
dove è contenuta nella
superficie.
Consideriamo la quadrica di equazione ridotta
dove
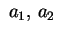 sono sono 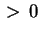 ; essa rappresenta, per quanto
detto, un cilindro con generatrici parallele all'asse ; essa rappresenta, per quanto
detto, un cilindro con generatrici parallele all'asse 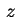 . Le
intersezioni con i piani . Le
intersezioni con i piani 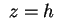 sono tutte ellissi uguali di
equazione sono tutte ellissi uguali di
equazione
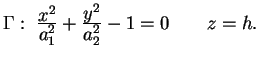
Da qui il nome cilindro ellittico.
L'equazione ridotta del cilindro
dove
 sono sono  , non è soddisfatta da alcun punto reale. , non è soddisfatta da alcun punto reale.
Da qui il nome cilindro ellittico immaginario.
Consideriamo ora il cilindro di equazione ridotta
dove
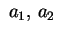 sono sono 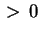 ; le intersezioni con i piani ; le intersezioni con i piani 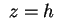 sono tutte iperboli uguali di equazione sono tutte iperboli uguali di equazione
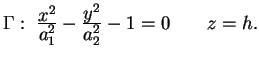
Da qui il nome cilindro iperbolico.
Considerando, infine, il cilindro di equazione ridotta
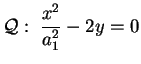
con 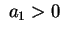 vediamo che le intersezioni con i piani vediamo che le intersezioni con i piani 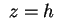 sono delle parabole tutte uguali di equazione sono delle parabole tutte uguali di equazione
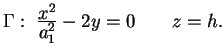
Da qui il nome cilindro parabolico.
|