|
Rappresentazione delle quadriche |
|||||||||||||
Iperboloide a due faldeSuperficie data dall'equazione ridotta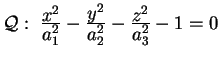
dove In particolare il piano 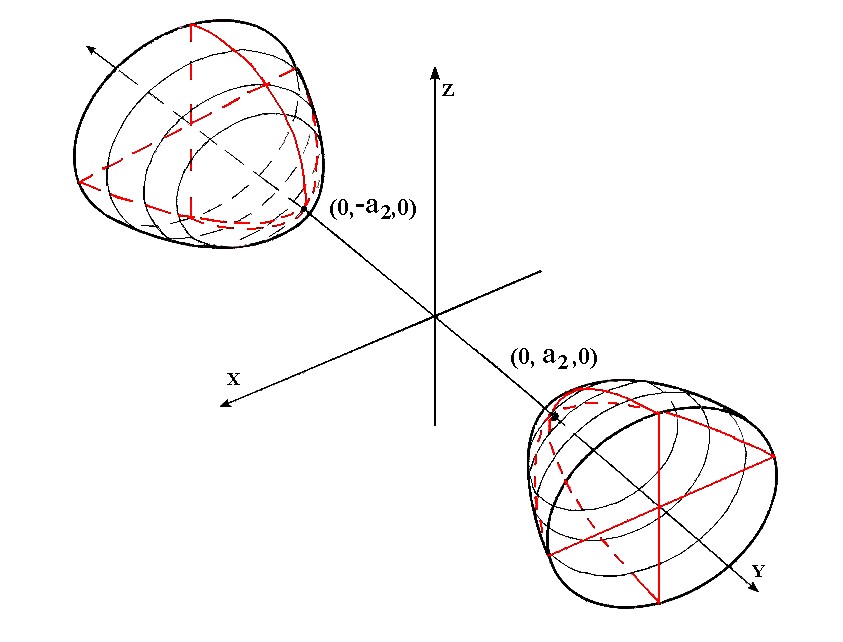
Iperboloide di rotazione a due falde Se 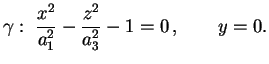
|
|
|
Rappresentazione delle quadriche |
|||||||||||||
Iperboloide a due faldeSuperficie data dall'equazione ridotta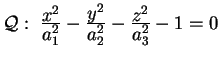
dove In particolare il piano 
Iperboloide di rotazione a due falde Se 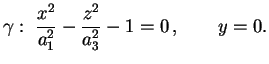
|
|