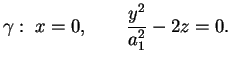Paraboloide ellittico
Superficie data dall'equazione ridotta
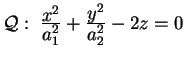
dove
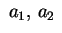 sono sono 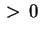 .
Sappiamo già che non esiste un centro di simmetria ed è
immediato verificare che solo l'asse .
Sappiamo già che non esiste un centro di simmetria ed è
immediato verificare che solo l'asse 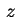 è asse di
simmetria. I piani di simmetria sono è asse di
simmetria. I piani di simmetria sono
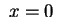 e e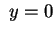 ;
non ce ne sono altri se ;
non ce ne sono altri se
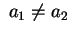 .
L'intersezione di .
L'intersezione di
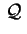 con i piani con i piani 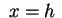 sono
parabole con asse parallelo all'asse sono
parabole con asse parallelo all'asse 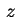 e vertice sulla
parabola e vertice sulla
parabola
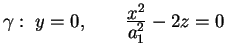 .
Analogamente l'intersezioni con i piani .
Analogamente l'intersezioni con i piani 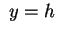 sono parabole
con asse parallelo all'asse sono parabole
con asse parallelo all'asse 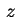 e vertice sulla parabola e vertice sulla parabola
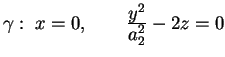 .
L'intersezione di .
L'intersezione di
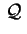 con i piani con i piani 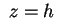 sono
ellissi per sono
ellissi per 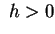 ,
che diventano sempre più grandi al crescere di ,
che diventano sempre più grandi al crescere di 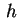 . .
L'intersezione con 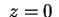 è un unico punto reale, mentre i
piani è un unico punto reale, mentre i
piani 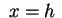 con con 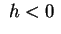 non intersecano non intersecano
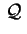 in nessun punto reale. Ciò vuol dire che in nessun punto reale. Ciò vuol dire che
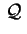 è tutta al di sopra del piano è tutta al di sopra del piano 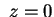 .
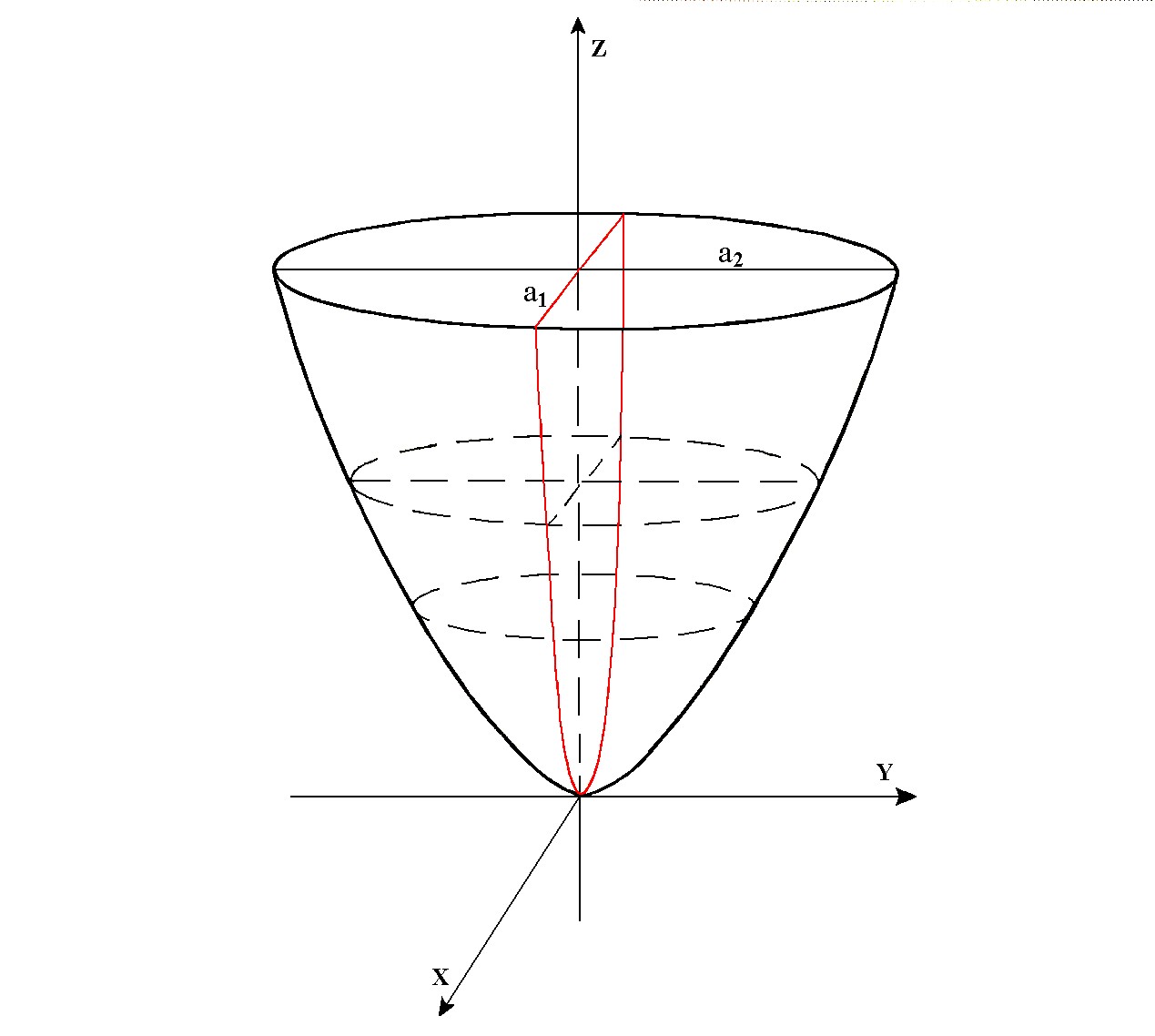
Paraboloide di rotazione
Se .
Paraboloide di rotazione
Se
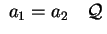 si ottiene facendo ruotare
attorno all'asse si ottiene facendo ruotare
attorno all'asse 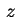 la parabola di equazione la parabola di equazione
|
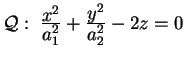
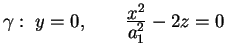 .
Analogamente l'intersezioni con i piani
.
Analogamente l'intersezioni con i piani 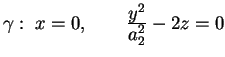 .
L'intersezione di
.
L'intersezione di
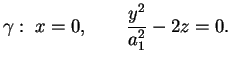

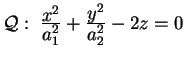
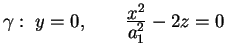 .
Analogamente l'intersezioni con i piani
.
Analogamente l'intersezioni con i piani 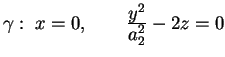 .
L'intersezione di
.
L'intersezione di