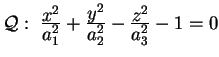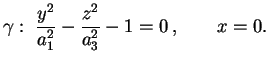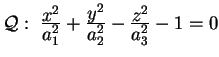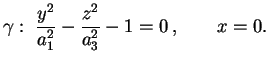Iperboloide a una falda
Superficie data dall'equazione ridotta
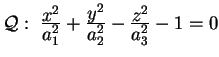
dove
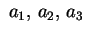 sono sono 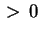 .
Con lo stesso procedimento usato per l'ellissoide si vede che i
piani coordinati, gli assi coordinati e .
Con lo stesso procedimento usato per l'ellissoide si vede che i
piani coordinati, gli assi coordinati e 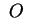 sono elementi di
simmetria di sono elementi di
simmetria di
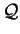 . Se . Se
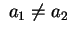 non ce ne
sono altri.
Le intersezioni con i piani non ce ne
sono altri.
Le intersezioni con i piani 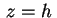 sono ellissi che
diventano sempre più grandi, e tendono all'infinito al crescere
di sono ellissi che
diventano sempre più grandi, e tendono all'infinito al crescere
di 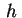 in valore assoluto.
Le intersezioni con i piani in valore assoluto.
Le intersezioni con i piani
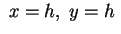 sono iperboli.
Queste iperboli sono equilatere se sono iperboli.
Queste iperboli sono equilatere se
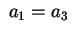 (per i piani (per i piani
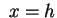 ) o ) o
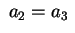 (per i piani (per i piani 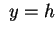 ). ).
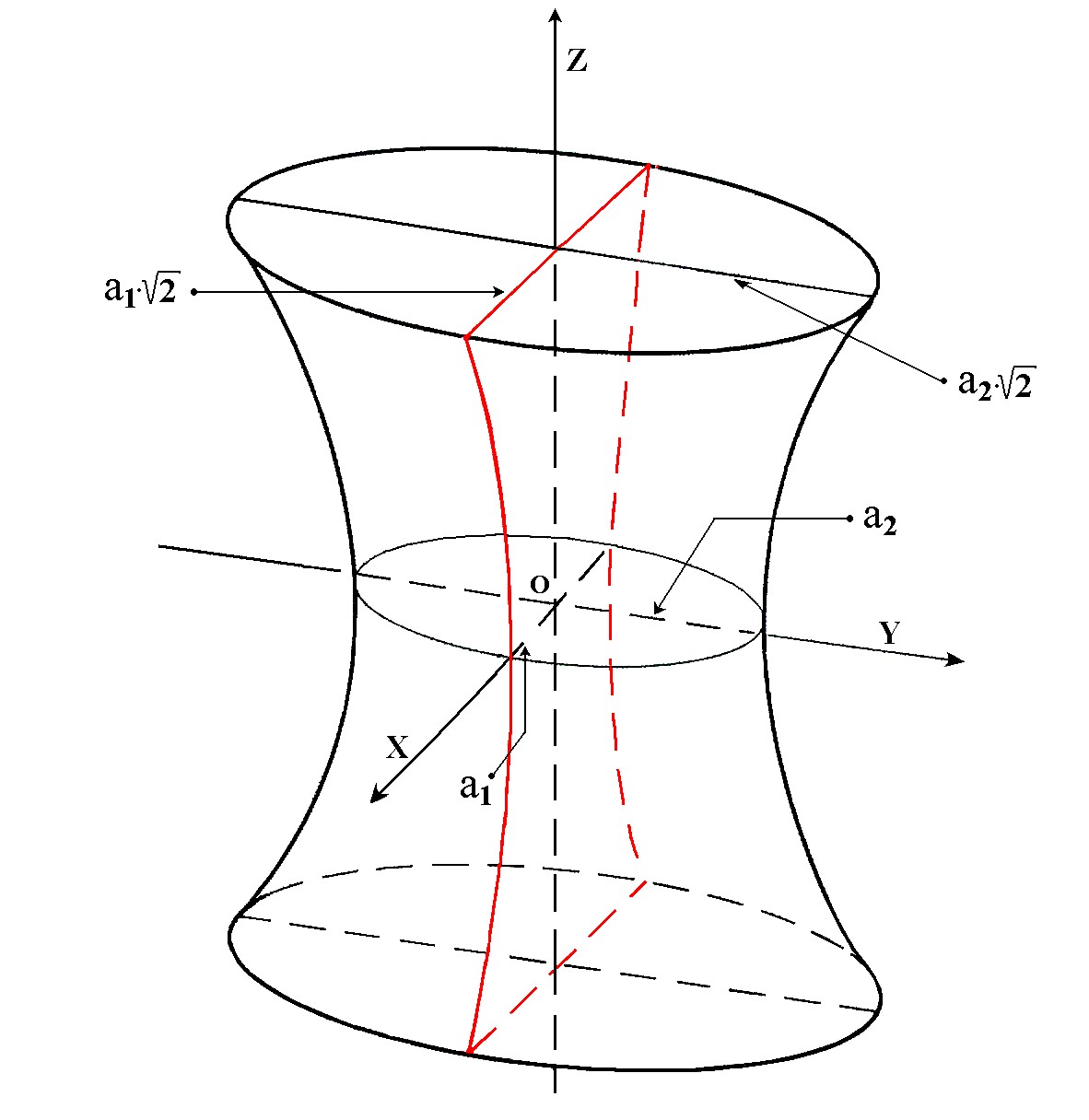
Iperboloide di rotazione a una falda
Se
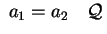 si ottiene facendo ruotare
attorno all'asse si ottiene facendo ruotare
attorno all'asse 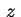 l'iperbole di equazione l'iperbole di equazione
|