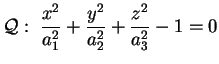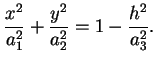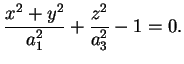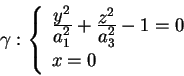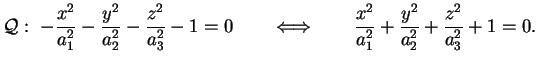Ellissoide
Superficie data dall'equazione ridotta
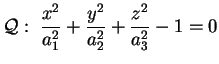
dove
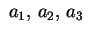 sono sono 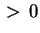 .
Sappiamo che è dotata di un unico centro .
Sappiamo che è dotata di un unico centro  di simmetria,
in questo caso di simmetria,
in questo caso
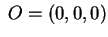 , quindi se , quindi se
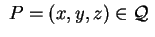 allora il simmetrico rispetto a allora il simmetrico rispetto a 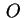 cioè cioè
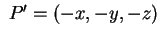 sta su sta su
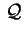 . .
Osserviamo che se
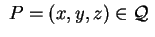 anche anche
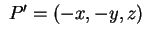 sta su sta su
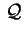 . Ciò vuol dire che se . Ciò vuol dire che se
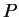 sta su sta su
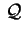 anche il simmetrico di anche il simmetrico di 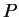 rispetto
all'asse rispetto
all'asse 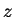 sta su
sta su
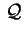 . Quindi l'asse . Quindi l'asse 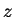 è asse di simmetria per è asse di simmetria per
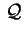 . .
In modo analogo si vede che anche gli altri assi coordinati sono
assi di simmetria.
Se
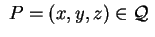 si vede che anche si vede che anche
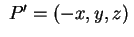 sta su sta su
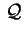 . Ciò vuol dire che se . Ciò vuol dire che se
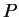 sta su sta su
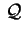 anche il simmetrico di anche il simmetrico di 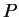 rispetto
al piano rispetto
al piano 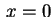 sta su sta su
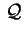 . Allora il piano . Allora il piano 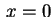 risulta essere
un piano di simmetria per risulta essere
un piano di simmetria per
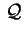 . .
Analogamente si vede che anche gli altri piani coordinati sono
piani di simmetria e non ce ne sono altri se
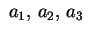 sono tutti diversi. sono tutti diversi.
Se intersechiamo l'ellissoide con il piano 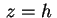 otteniamo
Si tratta di una ellisse (a punti reali) se otteniamo
Si tratta di una ellisse (a punti reali) se
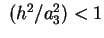 , ossia , ossia
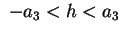 , di un solo punto reale se , di un solo punto reale se
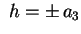 . L'intersezione non contiene punti reali se . L'intersezione non contiene punti reali se
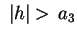 . In particolare . In particolare
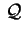 è tutta compresa
tra i due piani di equazione è tutta compresa
tra i due piani di equazione
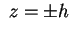 .
In modo analogo si ragiona per piani del tipo .
In modo analogo si ragiona per piani del tipo
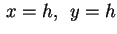 .
I numeri .
I numeri
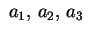 si chiamano semiassi
dell'ellissoide si chiamano semiassi
dell'ellissoide
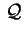 .
Da tutte queste considerazioni possiamo avere un'idea della forma
di .
Da tutte queste considerazioni possiamo avere un'idea della forma
di
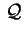 . .
Ellissoide di rotazione
Se due dei semiassi sono uguali,
 è una
superficie di rotazione attorno a uno degli assi. Ad esempio se è una
superficie di rotazione attorno a uno degli assi. Ad esempio se
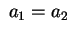 l'equazione di l'equazione di
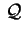 diventa:
quindi diventa:
quindi
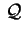 si ottiene ruotando l'ellisse
attorno all'asse si ottiene ruotando l'ellisse
attorno all'asse 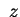 .
Se i tre semiassi sono uguali, .
Se i tre semiassi sono uguali,
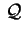 è una
superficie sferica di centro è una
superficie sferica di centro 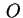 . .
Nella classificazione euclidea abbiamo trovato un'equazione del
tipo
Si vede subito che non esistono punti reali che soddisfano
l'equazione di
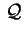 . Da qui il nome
Ellissoide immaginario. . Da qui il nome
Ellissoide immaginario.
|