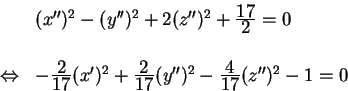Vediamo ora come applicare la teoria fin qui vista; cioè data
una quadrica
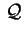 di equazione di equazione
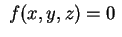 vediamo come operare per ridurla a forma canonica sia nello
spazio affine
vediamo come operare per ridurla a forma canonica sia nello
spazio affine
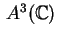 e e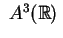 che in quello euclideo
che in quello euclideo 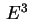 . Vediamo inoltre come
riconoscere, data . Vediamo inoltre come
riconoscere, data
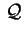 , di che tipo di quadrica si
tratta senza svolgere i calcoli, ma usando i valori degli
invarianti affini o euclidei. , di che tipo di quadrica si
tratta senza svolgere i calcoli, ma usando i valori degli
invarianti affini o euclidei.
Sia data la quadrica di equazione
cerchiamo la forma canonica affine che risulta essere equivalente
a
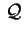 . .
La matrice associata a
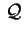 , e quella associata alla
parte quadratica sono:
risulta , e quella associata alla
parte quadratica sono:
risulta
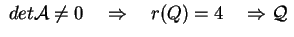 non degenere.
Cerchiamo l'affinità che manda non degenere.
Cerchiamo l'affinità che manda
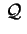 nella
quadrica nella
quadrica
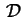 (forma canonica).
In pratica dobbiamo cercare un nuovo riferimento in cui (forma canonica).
In pratica dobbiamo cercare un nuovo riferimento in cui
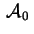 sia diagonale. Per far questo consideriamo la
forma quadratica sia diagonale. Per far questo consideriamo la
forma quadratica
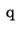 associata alla
matrice associata alla
matrice
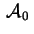 e scegliamo un primo vettore base e scegliamo un primo vettore base 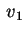 per il nuovo riferimento che soddisfi la condizione:
per il nuovo riferimento che soddisfi la condizione:
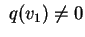 . .
Prendiamo, ad esempio,
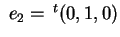 ; si ha ; si ha
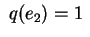 quindi va bene.
Calcoliamo ora quindi va bene.
Calcoliamo ora
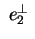 cioè
Prendiamo un secondo vettore cioè
Prendiamo un secondo vettore 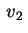 che, oltre a soddisfare
la precedente condizione, risulti anche tale che che, oltre a soddisfare
la precedente condizione, risulti anche tale che
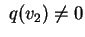 . Scegliamo come secondo vettore . Scegliamo come secondo vettore
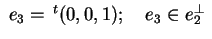 e si ha e si ha
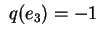 quindi va bene. quindi va bene.
Ripetendo le operazioni precedenti si calcola
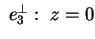 .
Cerchiamo ora il terzo vettore .
Cerchiamo ora il terzo vettore 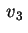 che formerà la nuova base. che formerà la nuova base.
Si deve avere:
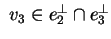 e al solito e al solito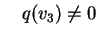 . Scegliamo come terzo
vettore . Scegliamo come terzo
vettore
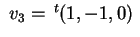 che soddisfa le condizioni;
risulta che soddisfa le condizioni;
risulta
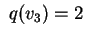 . .
Risulta quindi che
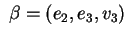 è una base
diagonalizzante per la forma quadratica che trasforma la matrice è una base
diagonalizzante per la forma quadratica che trasforma la matrice
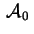 in
attraverso l'operazione in
attraverso l'operazione
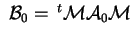 dove
Tutto ciò vuol dire che se effettuiamo nella quadrica una
trasformazione del tipo
si annulleranno i termini di secondo grado misti. Svolgendo i
calcoli si ottiene l'equazione
A questo punto bisogna far sparire i termini di primo grado.
Applichiamo il completamento dei quadrati alle variabili dove
Tutto ciò vuol dire che se effettuiamo nella quadrica una
trasformazione del tipo
si annulleranno i termini di secondo grado misti. Svolgendo i
calcoli si ottiene l'equazione
A questo punto bisogna far sparire i termini di primo grado.
Applichiamo il completamento dei quadrati alle variabili 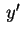 e e 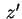 :
effettuando ora la sostituzione :
effettuando ora la sostituzione
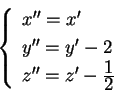 l'equazione della quadrica diventa l'equazione della quadrica diventa
A questo punto dobbiamo proseguire in base al tipo di
classificazione richiesto:
|
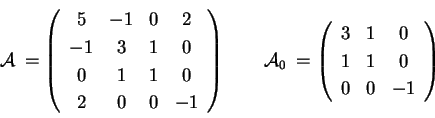
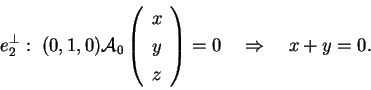
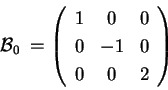
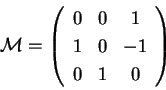
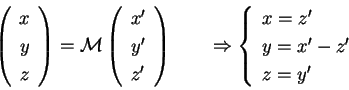
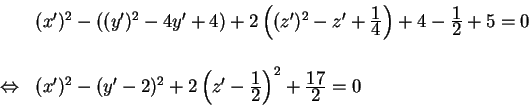
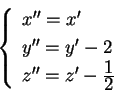 l'equazione della quadrica diventa
l'equazione della quadrica diventa