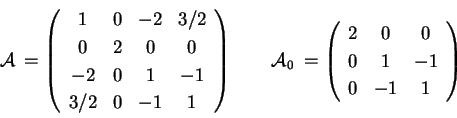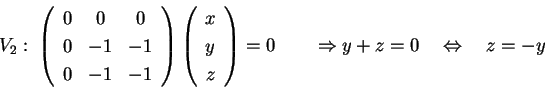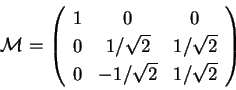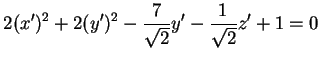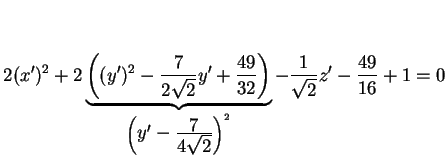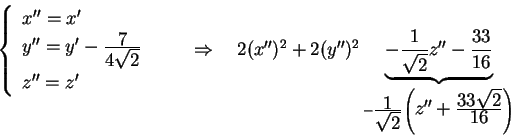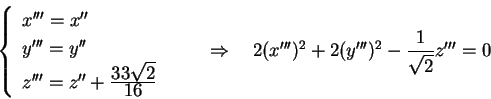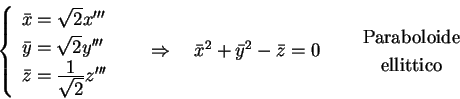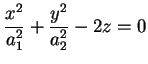Possiamo diagonalizzare
 attraverso una base di autovettori
(normalizzati nel caso euclideo) cioè mediante una matrice
attraverso una base di autovettori
(normalizzati nel caso euclideo) cioè mediante una matrice
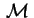 ortogonale. ortogonale.
Vediamo come effettuare tale diagonalizzazione:
Sia data la quadrica di equazione
cerchiamo la forma canonica.
La matrice associata a
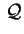 , e quella associata alla
parte quadratica sono:
risulta , e quella associata alla
parte quadratica sono:
risulta
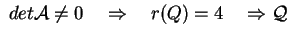 non degenere. Cerchiamo di
diagonalizzare non degenere. Cerchiamo di
diagonalizzare
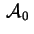 ; il suo polinomio
caratteristico è
ne risulta: ; il suo polinomio
caratteristico è
ne risulta:
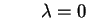 e e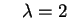 (con molteplicità 2). (con molteplicità 2).
Calcoliamo gli autovettori:
prendiamo i vettori
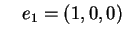 e e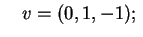 cioè
cioè
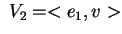 . .
Allo stesso modo si ottiene:
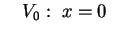 e e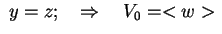 con con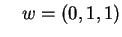 . .
[Nota: Quando ho un autospazio con dimensione 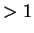 devo stare
attento a prendere vettori ortogonali all'interno
dell'autospazio.] devo stare
attento a prendere vettori ortogonali all'interno
dell'autospazio.]
A questo punto abbiamo
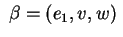 base ortogonale di
autovettori. Se vogliamo trovare la forma canonica euclidea
occorre normalizzare tale base (per quella affine non è
necessario).
Otteniamo la matrice che diagonalizza base ortogonale di
autovettori. Se vogliamo trovare la forma canonica euclidea
occorre normalizzare tale base (per quella affine non è
necessario).
Otteniamo la matrice che diagonalizza
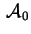 :
Mediante la solita sostituzione
si annulleranno i termini di secondo grado misti. Svolgendo i
calcoli si ottiene l'equazione
Applichiamo il completamento dei quadrati alla variabile :
Mediante la solita sostituzione
si annulleranno i termini di secondo grado misti. Svolgendo i
calcoli si ottiene l'equazione
Applichiamo il completamento dei quadrati alla variabile 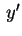 :
svolgendo la sostituzione, otteniamo:
effettuiamo un'altra sostituzione e otteniamo: :
svolgendo la sostituzione, otteniamo:
effettuiamo un'altra sostituzione e otteniamo:
Se quello che vogliamo è una classificazione affine reale
allora, attraverso un'ultima sostituzione, si ottiene
Se quello che vogliamo, invece, è una classificazione euclidea
allora ci fermiamo all'equazione
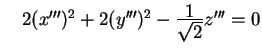 . .
Ora se ci riportiamo alla forma
otteniamo un paraboloide ellittico di equazione:
|