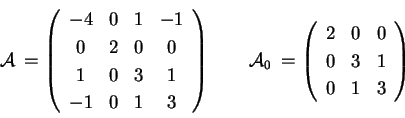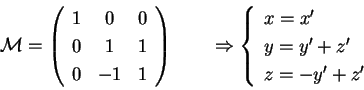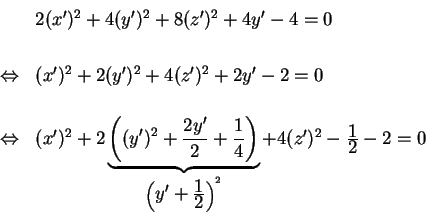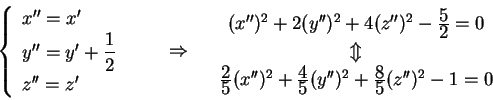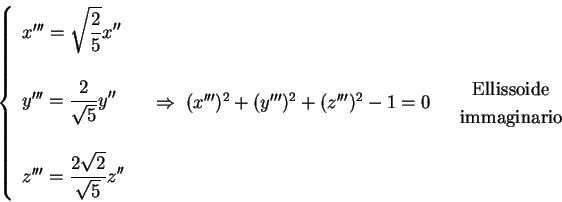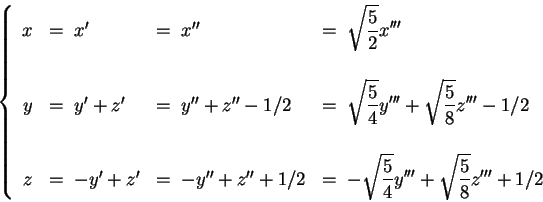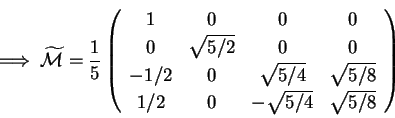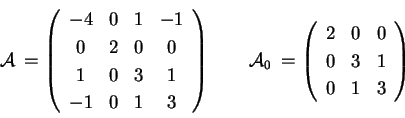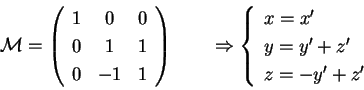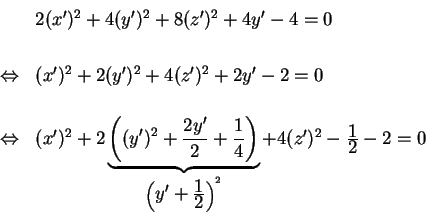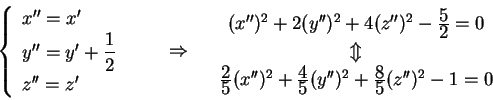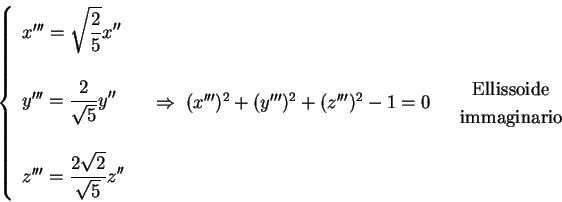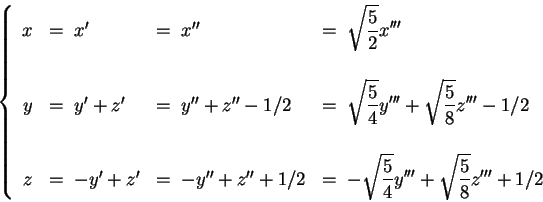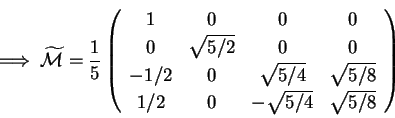Esempio 3:
Sia data una quadrica
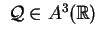 di
equazione:
trovare la forma canonica affine di
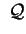 .
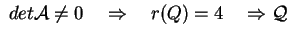 non degenere. Cerchiamo di
diagonalizzare non degenere. Cerchiamo di
diagonalizzare
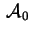 ; il suo polinomio
caratteristico è
ne risulta: ; il suo polinomio
caratteristico è
ne risulta:
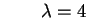 e e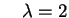 (con molteplicità 2). (con molteplicità 2).
Svolgendo i calcoli come nell'esempio precedente troviamo gli
autovettori:
Se vogliamo fare una classificazione euclidea dobbiamo
normalizzare i vettori mentre per quella affine non occorre.
Otteniamo così la matrice che diagonalizza
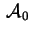 :
Con questa sostituzione :
Con questa sostituzione
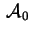 è una matrice
diagonale;
cioè sono spariti i termini di secondo grado misti.
La nuova equazione sarà
Effettuando la seguente sostituzione otteniamo:
Attraverso un'ultima sostituzione, si ottiene
Se vogliamo trovare la matrice è una matrice
diagonale;
cioè sono spariti i termini di secondo grado misti.
La nuova equazione sarà
Effettuando la seguente sostituzione otteniamo:
Attraverso un'ultima sostituzione, si ottiene
Se vogliamo trovare la matrice
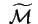 associata alla trasformazione che, nella quadrica
associata alla trasformazione che, nella quadrica
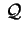 , porta l'equazione di partenza a quella canonica
basta riassumere le tre trasformazioni effettuate in una
sola.
( Nota ) , porta l'equazione di partenza a quella canonica
basta riassumere le tre trasformazioni effettuate in una
sola.
( Nota )
|