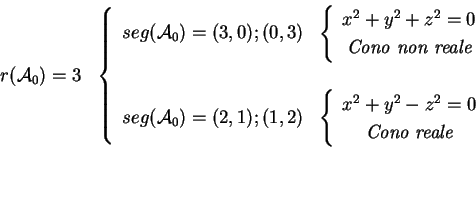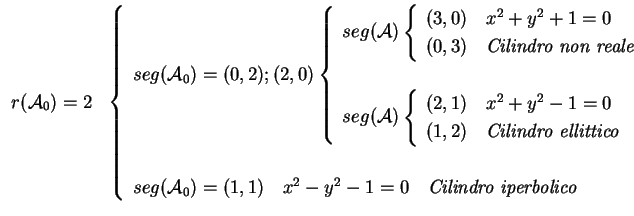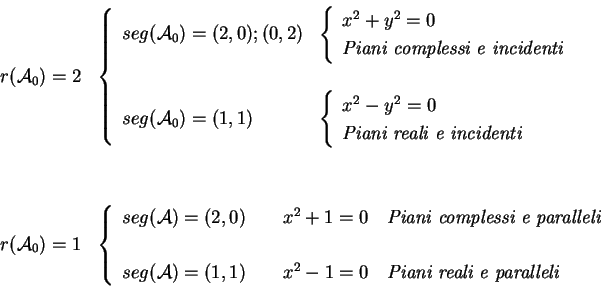È possibile riconoscere il tipo di una quadrica senza ridurla a forma canonica. In
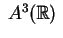 abbiamo 17 classi d'equivalenza di quadriche di cui:
Le prime sei sono quadriche non degeneri che possiamo
schematizzare nel seguente modo:
abbiamo 17 classi d'equivalenza di quadriche di cui:
Le prime sei sono quadriche non degeneri che possiamo
schematizzare nel seguente modo:
Le sei quadriche del secondo punto, cioe quelle con la rispettiva
matrice di rango 3 sono quadriche degeneri del tipo cono
o cilindro. Possiamo schematizzarle nel seguente modo:
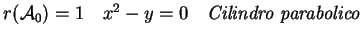
Le quadriche restanti sono formate da coppie di piani reali o
complesse coniugate. Nel caso di quadrica con rango 2 abbiamo:
Infine quando il rango della quadrica è uno si ha il piano
doppio di equazione 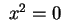 . .
Per calcolare
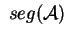 e e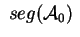 è conveniente calcolare il polinomio
caratteristico di tali matrici e poi applicare la regola di
Cartesio a tali polinomi. (Nota: il polinomio caratteristico ha
solo radici reali perchè gli autovalori di una matrice
simmetrica sono tutti reali.)
Naturalmente questo schema di riconoscimento delle quadriche è
valido anche nel caso euclideo. Sappiamo già che per una
quadrica non degenere in è conveniente calcolare il polinomio
caratteristico di tali matrici e poi applicare la regola di
Cartesio a tali polinomi. (Nota: il polinomio caratteristico ha
solo radici reali perchè gli autovalori di una matrice
simmetrica sono tutti reali.)
Naturalmente questo schema di riconoscimento delle quadriche è
valido anche nel caso euclideo. Sappiamo già che per una
quadrica non degenere in
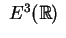 è possibile
calcolare la forma canonica utilizzando le formule introdotte nella
proposizione
della classificazione euclidea. è possibile
calcolare la forma canonica utilizzando le formule introdotte nella
proposizione
della classificazione euclidea.
|