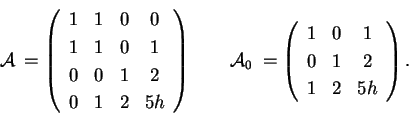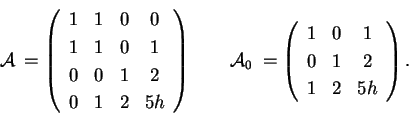Esempio 3:
Studiamo la quadrica di equazione
al variare del parametro reale 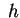 . .
Le matrici associate alla quadrica sono:
Si ha:
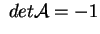 , quindi , quindi
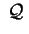 è
sempre non degenere. è
sempre non degenere.
Bisogna studiare i segni degli autovalori di
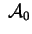 .
Il polinomio caratteristico di .
Il polinomio caratteristico di
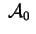 è:
Dobbiamo quindi esaminare le variazioni di segno nella successione
Si ha: è:
Dobbiamo quindi esaminare le variazioni di segno nella successione
Si ha:
Bisogna considerare quindi i seguenti casi:
Analizziamo alcuni casi:
- -
- Per
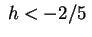 i segni dei coefficienti del p.c. sono i segni dei coefficienti del p.c. sono
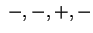 . Gli autovalori di . Gli autovalori di
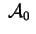 hanno quindi
segni hanno quindi
segni 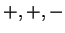 e una forma canonica di e una forma canonica di
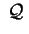 è è
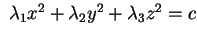 , con , con
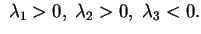 Inoltre Inoltre
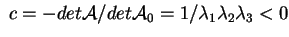 .
La quadrica è quindi un iperboloide a due falde. .
La quadrica è quindi un iperboloide a due falde.
- -
- Per
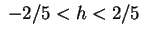 i segni dei coefficienti del p.c. sono i segni dei coefficienti del p.c. sono 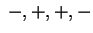 . Vi sono quindi due autovalori positivi e uno negativo. . Vi sono quindi due autovalori positivi e uno negativo.
 è allora un iperboloide a due falde (cfr. il caso
è allora un iperboloide a due falde (cfr. il caso 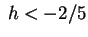 ). ).
- -
- Per
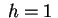 vi è un autovalore nullo. Inoltre i
segni dei coefficienti non nulli del p.c. sono vi è un autovalore nullo. Inoltre i
segni dei coefficienti non nulli del p.c. sono 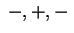 quindi gli altri due autovalori sono positivi. Una forma canonica
di
quindi gli altri due autovalori sono positivi. Una forma canonica
di
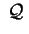 è è
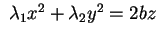 , con , con
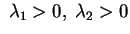 . Si tratta dunque di un
paraboloide ellittico. . Si tratta dunque di un
paraboloide ellittico.
- -
- Per
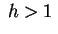 il p.c. non ha radici nulle e i segni dei suoi coefficienti sono il p.c. non ha radici nulle e i segni dei suoi coefficienti sono 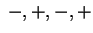 . Vi sono tre variazioni di segno quindi tre autovalori
positivi. Una forma canonica di . Vi sono tre variazioni di segno quindi tre autovalori
positivi. Una forma canonica di
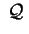 è è
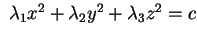 ; inoltre ; inoltre
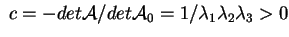 .
La quadrica è quindi un ellissoide reale. .
La quadrica è quindi un ellissoide reale.
Se si risolvono i casi mancanti si giunge alla conclusione che la
quadrica è un iperboloide a due falde per 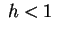 , un
paraboloide ellittico per , un
paraboloide ellittico per 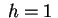 e un ellissoide reale per e un ellissoide reale per
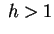 . .
|