Classificazione veloce delle quadriche

Esempio 2:

Riprendiamo l' esempio 2 visto in "Calcolo della forma normale"; abbiamo una quadrica di equazione

$\displaystyle \mathcal{Q}: \,2x^2+y^2+z^2-2yz-4y+3z+1=0;$

e le matrici associate sono:

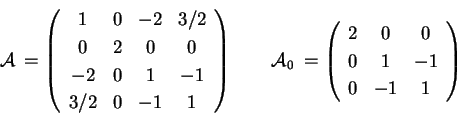
$\begin{displaymath} \mathcal{A}\: = \left( \begin{array}{cccc} 1 & 0 & -2 & 3... ... \\ 0 & 1 & -1 \\ 0 & -1 & 1 \\ \end{array} \right) \end{displaymath}$

risulta $\;det\mathcal{A}=-\frac{\displaystyle 1}{\displaystyle 2} \; \Rightarrow \; r(\mathcal{A})=4\;$ e $\;det\mathcal{A}_0=0;\;$ risulta $\; r(\mathcal{A}_0)=2.$
Sappiamo già che si tratta di un paraboloide e dal momento che $\;det\mathcal{A}<0 \;$ si tratta di un paraboloide ellittico.
Calcoliamo ora la forma canonica euclidea del paraboloide visto nel precedente esempio:
Il polinomio caratteristico di $\:\mathcal{A}_0 \:$ è:

$\displaystyle P_{\mathcal{A}_0}(\lambda)=(2-\lambda)((1-\lambda)^2-1)=(2-\lambda)^2\lambda.$

le radici sono: $\qquad \lambda = 0$ e $\quad \lambda = 2$ (con molteplicità 2).

Abbiamo quindi gli autovalori 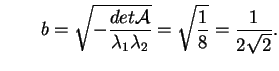$\;\lambda_1=2,\;\lambda_2=2,\;\lambda_3=0.$ La forma canonica può essere scritta nella forma:

$\displaystyle \lambda_1x^2+\lambda_2y^2-2bz=0$ dove $\displaystyle \qquad b=\sqrt{-\frac{det\mathcal{A}}{\lambda_1\lambda_2}} =\sqrt{\frac{1}{8}}=\frac{1}{2\sqrt{2}}.$

Il paraboloide ellittico ha dunque equazione

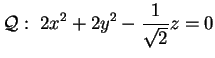
$\displaystyle \mathcal{Q}:\;2x^2+2y^2-\displaystyle \frac{1}{\sqrt{2}}z=0$

uguale a quella calcolata nell' esempio 2 visto in "Calcolo della forma normale".