|
Classificazione veloce delle quadriche |
|||||
|
Esempio 1:
Riprendiamo la quadrica dell' esempio 1
visto in "Calcolo della forma normale"; la sua equazione è:
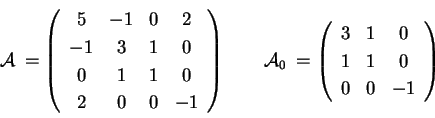
Il polinomio caratteristico di |
|
|
Classificazione veloce delle quadriche |
|||||
|
Esempio 1:
Riprendiamo la quadrica dell' esempio 1
visto in "Calcolo della forma normale"; la sua equazione è:
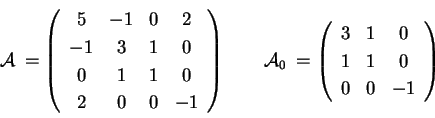
Il polinomio caratteristico di |
|