|
Calcolo della forma canonica |
||||
Caso Euclideo:Se cerchiamo la forma canonica nello spazio affine reale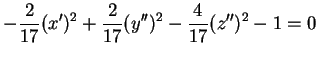
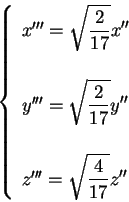
così da ottenere l'equazione |
|
|
Calcolo della forma canonica |
||||
Caso Euclideo:Se cerchiamo la forma canonica nello spazio affine reale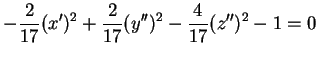
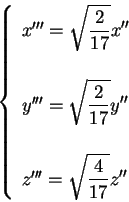
così da ottenere l'equazione |
|