

 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

|

|
6. PROPOSIZIONE Sia
DIMOSTRAZIONE
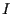 elemento neutro:
elemento neutro:
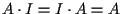

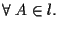
Siano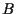 (e
(e 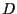 )
come nella definizione; poiché
)
come nella definizione; poiché
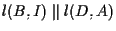 ,
segue che
,
segue che
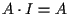 .
Nel calcolare
.
Nel calcolare 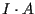 si osservi invece che la retta
si osservi invece che la retta 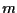 descritta nel secondo passo della definizione eguaglia la retta
descritta nel secondo passo della definizione eguaglia la retta 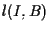 e quindi
e quindi 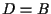 e
e 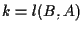 ;
e dunque
;
e dunque 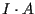 (determinato da
(determinato da 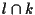 )
vale
)
vale 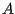 .
.
- esistenza dell'inverso:
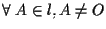 esiste un unico punto di
esiste un unico punto di 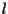 ,
che denoteremo
,
che denoteremo 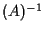 ,
tale che
,
tale che
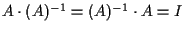 .
.
Siano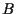 e
e 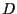 tali che
tali che
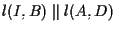 e
e
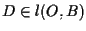 ;
sia
;
sia 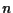 la retta passante per
la retta passante per 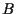 e parallela a
e parallela a 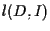 e poniamo per definizione
e poniamo per definizione 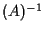 come il punto di intersezione di
come il punto di intersezione di 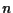 e
e 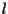 .
.
A questo punto basta moltiplicare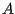 e
e 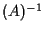 usando
usando 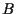 (e
(e 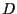 )
e
)
e 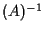 e
e 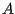 usando
usando 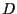 (e
(e 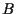 )
per ottenere in entrambi i casi il punto
)
per ottenere in entrambi i casi il punto 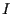 .
.
- associatività del prodotto:
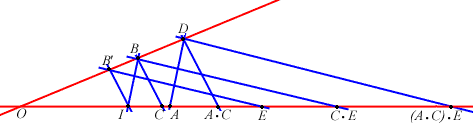
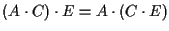

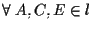 .
.
Si confronti con la prova dell'associatività della somma: prima moltiplichiamo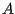 e
e 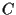 utilizzando
utilizzando 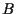 e
e 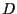 e poi moltiplichiamo
e poi moltiplichiamo 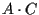 e
e 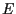 utilizzando un punto
utilizzando un punto 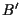 e
e
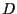 ove
ove 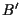 è stato scelto in modo tale che
è stato scelto in modo tale che
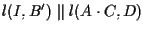 .
.
Moltiplichiamo ora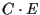 e utilizzando
e utilizzando 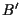 (e
(e 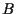 )
e alla fine moltiplichiamo
)
e alla fine moltiplichiamo 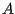 e
e 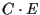 usando
usando 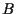 e (e
e (e 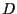 )
e otteniamo proprio che
)
e otteniamo proprio che
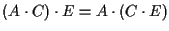 .
.
7. ESERCIZIO Sia
8. TEOREMA Sia
DIMOSTRAZIONE In virtú delle proposizioni 3 e 6 dobbiamo mostrare solamente che valgono le leggi distributive:
- 1.
-
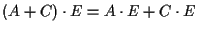

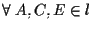 .
.

Infatti sia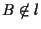 ;
calcoliamo
;
calcoliamo
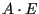 usando
usando 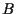 (e
(e 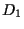 ),
),
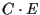 usando
usando 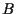 (e
(e 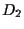 ),
),
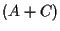 usando
usando 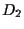 (e
(e 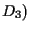 ,
,
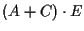 usando
usando 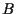 e
e 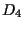 .
.
Sia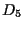 un punto sulla retta
un punto sulla retta
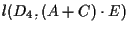 tale che
tale che
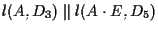 .
.
Servendoci del Teorema di Desargues relativamente alle terne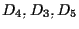 e
e
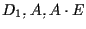 otteniamo che
otteniamo che
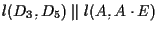 e questo mostra che
e questo mostra che
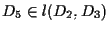 .
.
A questo punto sommiamo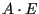 e
e 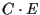 usando
usando 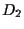 (e
(e 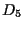 )
e notiamo che
)
e notiamo che
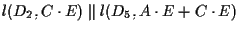 e questo significa che
e questo significa che
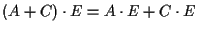 .
.
- 2.
- Proviamo, ancora con argomenti di tipo geometrico, che
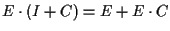

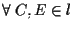 ;
successivamente con un'argomentazione di tipo algebrico seguirà che
;
successivamente con un'argomentazione di tipo algebrico seguirà che
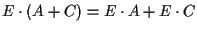

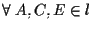 .
.
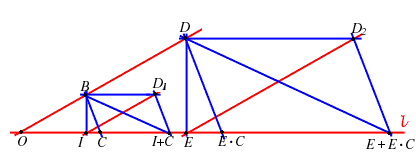
Sia dunque ;
calcoliamo
;
calcoliamo
 usando
usando  (e
(e 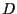 );
);
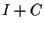 usando
usando 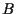 (e
(e 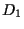 );
);
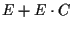 usando
usando
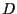 (e
(e 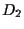 );
);
Usando il Teorema di Desargues B relativamente alle terne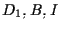 e
e 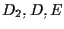 otteniamo che
otteniamo che
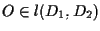 e infine, applicando il Teorema di Desargues alle terne
e infine, applicando il Teorema di Desargues alle terne
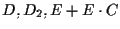 e
e 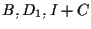 otteniamo che
otteniamo che
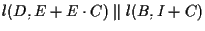 e quindi
e quindi
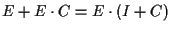 .
.
A questo punto siamo pronti per provare la seconda legge distributiva: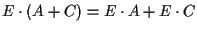 ;
;
se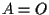 la prova è banale (da esercizio 7); se
la prova è banale (da esercizio 7); se 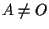 allora si ha la catena di uguaglianze:
allora si ha la catena di uguaglianze:
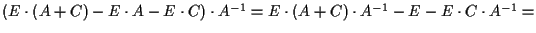
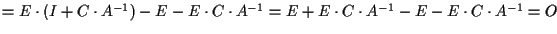 .
.
Questo implica (da esercizio 7) che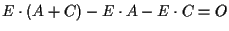 cioè proprio
cioè proprio
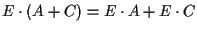 .
.
(abbiamo usato la distributività a destra nei primi 2 passaggi e la "particolare" distributività a sinistra nel terzo).
Abbiamo dunque provato che
![]() è un corpo, ma è naturale chiedersi: è anche un campo? ossia la moltiplicazione da noi definita è commutativa?
è un corpo, ma è naturale chiedersi: è anche un campo? ossia la moltiplicazione da noi definita è commutativa?
La risposta è, in generale, negativa ed essenzialmente i controesempi piú semplici (in realtà gli unici) possono venir esibiti costruendo piano affine coordinato (in cui le rette, ricordiamolo, sono i sottoinsiemi di
![]() che soddisfano ad equazioni lineari) su un corpo
che soddisfano ad equazioni lineari) su un corpo
![]() che non sia un campo; si può vedere che esso soddisfa gli assiomi A1, A2, A3 (come accennato) e inoltre esso soddisfa anche A4 -la prova è quasi del tutto identica a quella data nel caso di piani affini coordinati su campi- e dunque è un piano affine desarguesiano in cui possiamo definire una moltiplicazione fra punti; questa in sostanza è la moltiplicazione in
che non sia un campo; si può vedere che esso soddisfa gli assiomi A1, A2, A3 (come accennato) e inoltre esso soddisfa anche A4 -la prova è quasi del tutto identica a quella data nel caso di piani affini coordinati su campi- e dunque è un piano affine desarguesiano in cui possiamo definire una moltiplicazione fra punti; questa in sostanza è la moltiplicazione in
![]() e dunque non è commutativa.
e dunque non è commutativa.
L'esempio più semplice di corpo che non sia un campo è dato dall'anello dei quaternioni che in sé particolarmente semplice non è e quindi non mostreremo esplicitamente un controesempio.

 _______________
_______________
 __
__
 ________________________
________________________