

 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

|

|
Un insieme di assiomi è detto consistente se esiste un modello (o esempio) in cui tutti gli assiomi valgono. L'esistenza di un tale modello mostra che gli assiomi non sono contraddittori.
4. ESEMPIO IL PIANO COORDINATO REALE
Poniamo
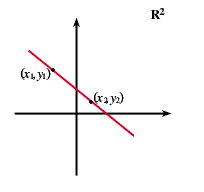 Questo è il consueto piano cartesiano della geometria analitica con cui il lettore dovrebbe avere una minima familiarità.
Questo è il consueto piano cartesiano della geometria analitica con cui il lettore dovrebbe avere una minima familiarità.
Non staremo a dimostrare dettagliatamente che in esso valgono gli assiomi A1,A2 e A3; ricordiamo solo i fatti principali:
- Innanzitutto equazioni proporzionali (per un fattore non nullo) individuano la stessa retta e viceversa due equazioni di una stessa retta sono necessariamente proporzionali; ciò segue immediatamente dalla teoria dei sistemi lineari.
- Dati
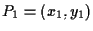 e
e
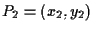 punti distinti di
punti distinti di
 ,
se
,
se 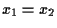 allora
allora 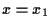 è l'equazione dell'unica retta passante per
è l'equazione dell'unica retta passante per 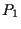 e
e 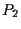 .
.
Se invece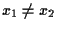 allora
allora
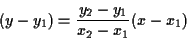
è l'equazione dell'unica retta passante per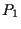 e
e 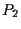 ;
;
si verifica direttamente che tali rette passano per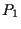 e
e 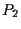 .
.
Bisogna verificare l'unicità:
se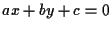 è l'equazione di una retta passante per
è l'equazione di una retta passante per 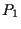 e
e 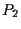 avremo le identità
avremo le identità
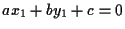 e
e
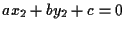 da cui
da cui
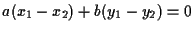 .
A questo punto supponiamo ad esempio
.
A questo punto supponiamo ad esempio
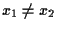 (fatto che implica
(fatto che implica 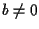 ), potremo scrivere
), potremo scrivere
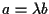 ove
ove
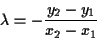
da cui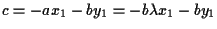 .
.
Abbiamo cioè un'equazione iniziale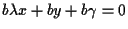 ove
ove
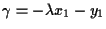 cioè se una retta passa per
cioè se una retta passa per 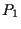 e
e 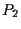 allora esiste
allora esiste 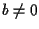 tale che un'equazione della retta sia
tale che un'equazione della retta sia
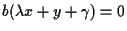 ove le costanti
ove le costanti 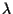 e
e 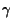 dipendono solo da
dipendono solo da 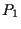 e
e 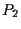 ;
siccome equazioni proporzionali individuano la stessa retta abbiamo finito.
;
siccome equazioni proporzionali individuano la stessa retta abbiamo finito.
Similmente si conclude nel caso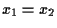 e in definitiva in
e in definitiva in
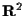 A1 vale.
A1 vale.
- Se
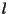 è una retta di equazione
è una retta di equazione 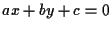 segue dalla teoria dei sistemi lineari che ogni retta parallela ad
segue dalla teoria dei sistemi lineari che ogni retta parallela ad 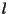 può venir rappresentata tramite un'equazione del tipo
può venir rappresentata tramite un'equazione del tipo 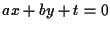 con
con
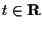 arbitrario (cioè l'insieme delle rette di equazione
arbitrario (cioè l'insieme delle rette di equazione 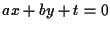 al variare di
al variare di
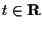 descrive il fascio di rette parallele a
descrive il fascio di rette parallele a 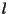 ); per cui se
); per cui se
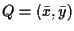 è un punto di
è un punto di
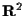 abbiamo che, imponendo il passaggio per
abbiamo che, imponendo il passaggio per  ,
si ottiene
,
si ottiene
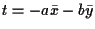 e dunque la retta
e dunque la retta 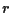 di equazione
di equazione
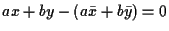 è l'unica parallela a
è l'unica parallela a 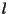 passante per
passante per 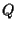 e ciò dimostra in definitiva che in
e ciò dimostra in definitiva che in
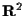 A2 vale.
A2 vale.
- La verifica di A3 è banale.
Il fatto interessante è che per mostrare la validità degli assiomi A1,A2 e A3 non abbiamo usato nessuna proprietà caratterizzante i numeri reali (proprietà che sono essenziali per mostrare asserzioni di natura geometrica intuitivamente altrettanto semplici, ad esempio che una circonferenza interseca sempre una retta passante per il suo centro).
Sono state utilizzate esclusivamente le usuali proprietà algebriche, cioè il fatto che
Noi sappiamo già che un "piano affine algebrico" è "in sostanza" (a meno cioè di isomorfismi affini) un

 _______________
_______________
 __
__
 ________________________
________________________