

 |
 |
 |
 |
 |
 |
 |
 |

|

|
Il ruolo di ogni assioma può essere chiarificato esibendo esempi che soddisfano a due di essi ma non a tutti e tre: se possiamo trovare un modello in cui, diciamo, A1 e A2 valgono ma non A3 allora ciò significherà che A3 non può essere dedotto usando solo i primi due assiomi; in tal caso si dice che A3 è indipendente da A1 e A2.
Un sistema di assiomi in cui ciascuno è indipendente dagli altri è detto sistema di assiomi indipendenti; i seguenti tre esempi mostrano che A1, A2 e A3 costituiscono un sistema di assiomi indipendenti (clicca qui per visualizzare la pagina contenente gli enunciati degli assiomi).
3. OSSERVAZIONE
- INDIPENDENZA di A1
Sia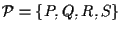 e
e
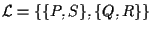 .
.
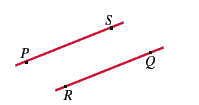
Dato che non esiste nessuna retta passante per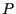 e
e 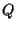 ,
A1 non vale; invece A2 vale come si puo provare per tentativi, ad esempio
,
A1 non vale; invece A2 vale come si puo provare per tentativi, ad esempio
 e l'unica retta passante per
e l'unica retta passante per 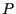 è
è 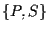 che a
che a 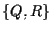 è parallela; A3 vale in quanto abbiamo due rette distinte contenenti ciascuna due punti distinti.
è parallela; A3 vale in quanto abbiamo due rette distinte contenenti ciascuna due punti distinti.
Si noti che nella rappresentazione grafica che abbiamo dato di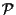
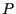 e
e 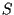 sono connessi da un segmento per indicare che essi sono collineari, ma in effetti non ci sono altri punti sulla retta
sono connessi da un segmento per indicare che essi sono collineari, ma in effetti non ci sono altri punti sulla retta 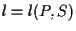 diversi da questi ultimi.
diversi da questi ultimi.
- INDIPENDENZA di A2
Sia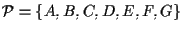 e
e
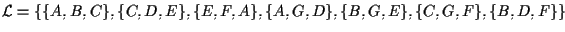 .
.
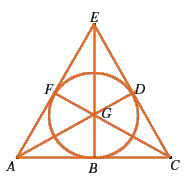
Esistono 21 coppie di punti e 21 coppie di rette (coppie non ordinate di elementi distinti, s'intende) e si può mostrare, esaminando tutti i casi possibili -pur sempre in numero finito-, che ogni coppia di punti giace su una e una sola retta (ad esempio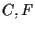 sta su
sta su 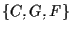 )
e quindi A1 vale.
)
e quindi A1 vale.
A2 invece non vale, addirittura in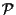 non esistono coppie di rette parallele -
non esistono coppie di rette parallele -
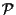 in effetti è un piano proiettivo- come si può verificare controllando su ciascuna delle 21 coppie di rette, ad esempio
in effetti è un piano proiettivo- come si può verificare controllando su ciascuna delle 21 coppie di rette, ad esempio
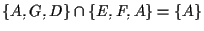 .
.
A3 vale in quanto abbiamo 3 punti distinti su ciascuna retta e 7 rette distinte.
A proposito della rappresentazione grafica si ha ancora che la retta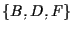 ,
da noi rappresentata tramite una circonferenza, sembra intersecare la retta
,
da noi rappresentata tramite una circonferenza, sembra intersecare la retta 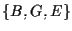 in un punto tra
in un punto tra 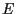 e
e 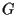 .
Invece esse si intersecano solo in
.
Invece esse si intersecano solo in 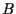 .
.
Anche questo piano non può essere rappresentato su una superficie piatta usando segmenti per le rette poiché esso non fa parte della geometria euclidea.
Acenniamo a come quello presentato sia un esempio di piano proiettivo (precisamente esso è il piú piccolo piano proiettivo ed è detto piano di Fano dal nome del matematico che lo introdusse nel 1892) e in effetti ogni spazio proiettivo soddisfa gli assiomi A1 e A3 ma non A2.
- INDIPENDENZA di A3
Poniamo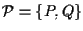 e
e
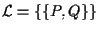 ;
A1 vale chiaramente e vale anche A2; infatti non possiamo trovare un punto non giacente sull'unica retta e dunque non c'è nulla da verificare; A3 chiaramente non vale.
;
A1 vale chiaramente e vale anche A2; infatti non possiamo trovare un punto non giacente sull'unica retta e dunque non c'è nulla da verificare; A3 chiaramente non vale.

 _______________
_______________
 __
__
 ________________________
________________________