|
 |
 |
 |
 |
 |
 |
 |

|

|
1. DEFINIZIONE Un piano affine è un insieme non vuoto
- Se
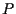 è un punto e
è un punto e 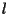 una retta e
una retta e 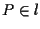 diciamo indifferentemente che
diciamo indifferentemente che 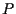 incide o giace su
incide o giace su 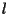 o che
o che 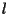 passa per
passa per 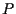 .
.
- Se
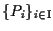 è una famiglia di punti di
è una famiglia di punti di
 ed esiste una retta
ed esiste una retta 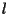 tale che
tale che
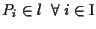 ,
allora diremo che i punti
,
allora diremo che i punti 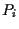 sono allineati o collineari.
sono allineati o collineari.
- Se due rette
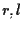 sono coincidenti oppure disgiunte allora sono dette parallele;
sono coincidenti oppure disgiunte allora sono dette parallele;
altrimenti (cioè se sono distinte e si intersecano) sono dette incidenti.
Se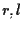 sono incidenti e
sono incidenti e
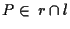 allora si dice che
allora si dice che 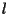 e
e 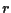 incidono in
incidono in 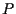 .
.
- Nell'insieme
 la relazione essere rette parallele è banalmente una relazione di equivalenza; le classi di equivalenza cosí determinate sono dette fasci di rette parallele; un fascio di rette parallele è dunque un insieme massimale di rette parallele o equivalentemente un insieme consistente di una retta e di tutte le parallele ad essa.
la relazione essere rette parallele è banalmente una relazione di equivalenza; le classi di equivalenza cosí determinate sono dette fasci di rette parallele; un fascio di rette parallele è dunque un insieme massimale di rette parallele o equivalentemente un insieme consistente di una retta e di tutte le parallele ad essa.
Secondo la terminologia appena introdotta potremo dire che:
- A1 afferma che in un piano affine per due punti distinti
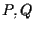 passa un'unica retta
passa un'unica retta 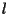 ,
e scriveremo
,
e scriveremo 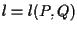 .
.
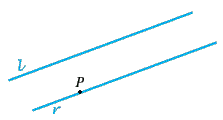
- A2 afferma che in un piano affine vale il V postulato di Euclide (o postulato delle parallele): assegnati un punto
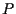 e una retta
e una retta 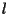 esiste un'unica retta
esiste un'unica retta 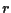 parallela a
parallela a 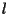 e passante per
e passante per 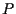 .
.
Infatti se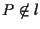 abbiamo esattamente il contenuto di A2; se invece
abbiamo esattamente il contenuto di A2; se invece 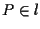 allora
allora 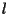 è l'unica parallela a se stessa passante per
è l'unica parallela a se stessa passante per 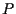 ,
infatti per definizione due rette parallele non coincidenti sono disgiunte.
,
infatti per definizione due rette parallele non coincidenti sono disgiunte.
- A3 afferma che in un piano affine su ogni retta stanno almeno due punti distinti e che esistono almeno due rette distinte.

 _______________
_______________
 __
__
 ________________________
________________________